Download Applying Bayesian networks to modeling of cell signaling pathways

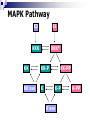
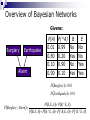
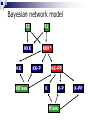
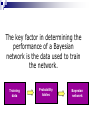
Applying Bayesian
networks to modeling
of cell signaling
pathways
Kathryn Armstrong and
Reshma Shetty
Outline
Biological model system (MAPK)
 Overview of Bayesian networks
 Design and development
 Verification
 Correlation with experimental data
 Issues
 Future work

MAPK Pathway
E2
E1
KKK
KKK*
KK
KK-P
KK’ase
K
KK-PP
K-P
K’ase
K-PP
Overview of Bayesian Networks
Givens:
Burglary
Earthquake
Alarm
P(A)
0.01
0.80
0.10
0.90
P(^A)
0.99
0.20
0.90
0.10
B
No
Yes
No
Yes
E
No
No
Yes
Yes
P Burglary   0.01
P Earthquake  0.01
P B, E, A  PB,^E, A
PBurglary | Alarm 
PB, E, A  P B,^E, A  P^B, E, A  P ^B,^E, A

Bayesian network model
E2
E1
KKK
KK
KK’ase
KKK*
KK-P
KK-PP
K
K-P
K’ase
K-PP
Simplifying Assumptions
Normalized concentrations of all
species
 Discretized continuous concentration
curves at 20 states


Considered steady-state behavior
The key factor in determining the
performance of a Bayesian
network is the data used to train
the network.
Training
data
Probability
tables
Bayesian
network
Network training I: Data source
Current experimental data sets were
not sufficient to provide enough
information
 Relied on ODE model to generate
training set (Huang et al.)
 Captured the essential steady-state
behavior of the MAPK signaling
pathway

Network training II: Poor data
variation
Network training III: incomplete
versus complete data sets
1D x 4
E1
4D
E2
MAPKPase MAPKKPase
Time = (# samples) x 4
Time = (# samples)4
Verification: P(Kinase | E1, P’ases)
Huang et al.
Bayesian network
Verification: P(E1 | MAPK-PP, P’ases)
Correlation with experimental data
C.F. Huang and J.E. Ferrell, Proc. Natl. Acad. Sci. USA 93, 10078 (1996).
Correlation with experimental data
J.E. Ferrell and E.M. Machleder, Science 280, 895 (1998).
Where does our Bayesian
network fail?
Where does our Bayesian
network fail?
Inference from incomplete data
E2
E1
KKK
KK
KK’ase
KKK*
KK-P
KK-PP
K
K-P
K’ase
K-PP
Future work





Time incorporation to represent signaling
dynamics
Continuous or more finely discretized
sampling and modeling of node values
Priors
Bayesian posterior
Structure learning
Open areas of research
Should steady state behavior be
modeled with a directed acyclic
graph?
 Cyclic networks

Theoretically impossible
Hard, but doable
Need an alternate way to
represent feedback loops
Why use a Bayesian network?
ODE’s require detailed kinetic and
mechanistic information on the
pathway.
 Bayesian networks can model
pathways well when large amounts
of data are available regardless of
how well the pathway is understood.

Acknowledgments
Kevin Murphy
 Doug Lauffenburger
 Paul Matsudaira
 Ali Khademhosseini
 BE400 students

References









http://www.cs.berkeley.edu/~murphyk/Bayes/bayes.html
http://www.ai.mit.edu/~murphyk/Software/BNT/usage.html
A.R. Asthagiri and D.A. Lauffenburger, Biotechnol. Prog. 17, 227 (2001).
A.R. Asthagiri, C.M. Nelson, A.F. Horowitz and D.A. Lauffenburger, J. Biol.
Chem. 274, 27119 (1999).
J.E. Ferrell and R.R. Bhatt, J. Biol. Chem. 272, 19008 (1997).
J.E. Ferrell and E.M. Machleder, Science 280, 895 (1998). C.F. Huang and
J.E. Ferrell, Proc. Natl. Acad. Sci. USA 93, 10078 (1996). F. V. Jensen.
Bayesian Networks and Decision Graphs. Springer: New York, 2001.
K.A. Gallo and G.L. Johnson, Nat. Rev. Mol. Cell Biol. 3, 663 (2002). K.P.
Murphy, Computing Science and Statistics. (2001).
S. Russell and P. Norvig. Artificial Intelligence: A Modern Approach.
Prentice Hall: New York, 1995.
K Sachs, D. Gifford, T. Jaakkola, P. Sorger and D.A. Lauffenburger, Science
STKE 148, 38 (2002).
Network training IV: final data
set
E1
E2 (P’ase)
MAPKKPase
MAPKPase
MAPK-PP
0
0
0
0
0
0
0
0
1
0
0
0
1
0
0
0
0
1
1
0
0
1
0
0
0
0
1
0
1
0
0
1
1
0
0
0
1
1
1
0
1
0
0
0
1
1
0
0
1
1
1
0
1
0
1
1
0
1
1
0
1
1
0
0
1
1
1
0
1
0
1
1
1
0
0
1
1
1
1
0
Network training V: Final
concentration ranges
Network training III: Observation
of all input combinations
1D Visualization
E1
E2
3D Visualization
E2
E1
MAPKPase MAPKKPase
MAPKKPase
4D Visualization
2D Visualization
Time = (# samples)4