Download Lesson Plan Format

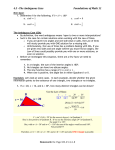
HW-The Law of Sines WS (19-27 odd) &
WS 1 (1-3 & 6)
www.westex.org HS, Teacher Website
2-24-14
Warm up—Geometry H
1. What is the equation that you use for Law of
Sines?
GOAL:
I will be able to:
use law of sines to
1. determine how many triangles are possible.
2. find the area of a triangle.
HW-The Law of Sines WS (19-27 odd) &WS 1 (1-3 & 6)
www.westex.org
HS, Teacher Website
Name _________________________
Date ________
Geometry H
8.5 Law of Sines (continued)
GOAL:
I will be able to:
use law of sines to:
1. determine how many triangles are possible.
2. find the area of a triangle.
In Geometry, we found that we could prove two triangles congruent using:
SAS - Side, Angle, Side
ASA - Angle, Side, Angle
We also discovered that _____
AAS - Angle, Angle, Side
did not work to prove triangles congruent.
SSS - Side, Side, Side
HL - Hypotenuse Leg for Right Triangles.
By definition, the word _______________ means open to two or more interpretations.
Such is the case for certain solutions when working with the Law of Sines.
•If you are given two angles and one side (ASA or AAS), the Law of Sines will
nicely provide you with ONE solution for a missing side.
•Unfortunately, the Law of Sines has a problem dealing with SSA. If you are
given two sides and one non included angle, the Law of Sines could possibly provide
you with ______ or _________ solutions, or even _____ solution.
Before we investigate this situation, there are a few facts we need to consider.
Facts we need to consider:
1. In a triangle, the sum of the interior angles is 180º.
2. No triangles can have two obtuse angles.
3. The sine function has a range of-1 to 1.
4. If the Sin X = positive decimal < 1, the angle can lie in the
first quadrant (acute <) or in the second quadrant (obtuse <).
Let's look at some cases. In each example, decide whether the given information points to the
existence of one triangle, two triangles or NO triangles.
Example 1: In ∆ABC, a = 20, c = 16, and m<A = 30º. How many distinct triangles can be drawn
given these measurements? Let’s draw a picture and use the Law of Sines:
m<C = sin-1 (0.4) = 24º (to the nearest degree) - in Quadrant I.
Sine is also positive in Quadrant II.
If we use the reference angle 24º in Quadrant II, the angle C is 156º.
But, with m<A = 30º and m<C = 156º the sum of the angles would exceed 180º. Not possible!!!!
Therefore, m<C = 24º, m<A = 30º, and m<B = 126º and only _____ __________ is possible.
Example 2: In, ∆ABC a = 7, c = 16, and m<A = 30º. How many distinct triangles can be drawn
given these measurements? Let’s draw a picture and use the Law of Sines:
Since sin C must be < 1, no angle exists for angle C.
_____ __________ exists for these measurements.
Example 3: In ∆ABC, a = 10, b = 16, and m<A = 30º. How many distinct triangles can be drawn
given these measurements? Let’s draw a picture and use the Law of Sines:
m<B = sin-1(.8) = 53º (to the nearest degree). Angles could be 30º, 53º, and 97º : sum 180º
The angle from Quadrant II could create angles 30º, 127º, and 23º : sum 180º
_____ __________ possible.
This example is the _______________ __________. The information given is the postulate
SSA but the two triangles that were created are clearly not congruent. We have two triangles
with two sides and the non-included angle congruent, but the triangles are not congruent to
each other.