* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Angles - MrLinseman
Penrose tiling wikipedia , lookup
Golden ratio wikipedia , lookup
Line (geometry) wikipedia , lookup
Rotation formalisms in three dimensions wikipedia , lookup
Technical drawing wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Multilateration wikipedia , lookup
Rational trigonometry wikipedia , lookup
History of trigonometry wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Trigonometric functions wikipedia , lookup
Integer triangle wikipedia , lookup
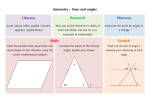
Name: Date: MPM 1D Lesson ANGLES COMPLEMENTARY ANGLES A Complementary angles add up to 90 C B D SUPPLEMENTARY ANGLES supplementary angles add up to B 180 A C ACUTE ANGLE acute angles are less than 90 OBTUSE ANGLE obtuse angles are between 90 and 180 REFLEX ANGLE reflex angles are between 180 and 360 OPPOSITE ANGLES OPPOSITE ANGLES EXAMPLE opposite angles are equal 112 A C A D B and B D y x z C x ________ y __________ z __________ ANGLES OF 2 PARALLEL LINES ALTERNATE ANGLES angles between two lines and are on opposite sides of a transversal that intersects the two lines. alternate angles are equal. alternate angles form a _______________ pattern or a _______________ pattern Example: x x 132 x x x x ____________ CORRESPONDING ANGLES angles that are on the same side of a transversal and on the same side of each line corresponding angles are equal they form an ___________, ____________, ___________ or __________ pattern. 126 Example: x x ____________ INTERIOR ANGLES Angles that are between two lines and are on the same side of a transversal that intersects the two lines They are supplementary angles, therefore, they add up to 180 They form a ___________ or ___________ pattern. Example: x 126 x y 180 x y x ____________ 3 CLASSIFYING TRIANGLES SCALENE TRIANGLE BY LENGTH ISOSCELES TRIANGLE no equal sides ACUTE TRIANGLE BY SIDES EQUILATERAL TRIANGLE 3 equal sides 2 equal sides CLASSIFYING TRIANGLES OF SIZE OF RIGHT TRIANGLE ANGLES RIGHT ISOSCELES TRIANGLE A B C all angles are less than 90 OBTUSE TRIANGLE the triangles has one obtuse angle i.e. one angle is greater that 90 the triangles has one 90 -angles ACUTE SCALENE TRIANGLE all angles are less than 90 and the sides are all different in length the triangles has one 90 -angles and two equal sides