* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Problem Set #1 - Purdue College of Engineering
Computational fluid dynamics wikipedia , lookup
Navier–Stokes equations wikipedia , lookup
Hydraulic machinery wikipedia , lookup
Aerodynamics wikipedia , lookup
Fluid thread breakup wikipedia , lookup
Derivation of the Navier–Stokes equations wikipedia , lookup
Reynolds number wikipedia , lookup
Blower door wikipedia , lookup
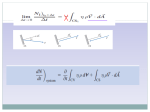
AAE333 Fall 2010 Homework 4 Due: Monday Sept 20 10% bonus if turned in on Friday 9/17/10 1. Consider a tank of water 1m deep. At the bottom of the tank is a square door, 2 cm on each side, which is hinged along the top edge so the bottom is free to rotate outward from the tank. The tank is open at the top to 1 atm air. The door connects the tank to a pressurized line full of air. Determine the line pressure required to keep the door closed for two situations: a. The door hangs vertically b. The door hangs at a 45deg angle to the horizontal (and vertical) 2. Consider a pan which is 2cm deep, 10cm long and 5 cm wide. The pan is half filled with water, 1cm deep. This pan is placed on a cart which is subjected to a uniform acceleration “a” along the long axis of the pan (10cm). Determine how big “a” would have to be (in “g’s” ) to make the water slosh out the rear end of the pan. 3. Salt water exits a 1cm by 1cm square hole at a speed of 2cm/s. The salt content is 0.2% by weight. What is the mass flow rate of salt coming out the hole (ie. gm/sec) ? 4. Given a velocity field u 2 xe x 3 ye y Kze z , where K is some constant and velocities are measured in m/s. Find the rate of expansion of a fluid particle (i.e. the fractional increase in volume per second). What value would K have to have for the fluid to be incompressible? 5. For the same velocity field given in Pb 4, determine the total volume per second of fluid leaving a cube with each edge .2 m long, with its six faces at x=0, x=.2, y=0, y=.2, z=0 and z=.2 respectively. What is the this volume flow rate if the fluid is incompressible? AAE333 Fall 2010