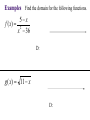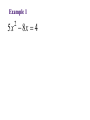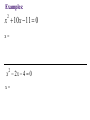Download 1.1 Basic Equations

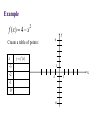
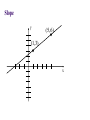
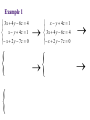
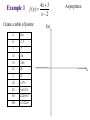
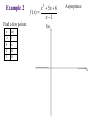
Solving Linear Equations

Solving equation = finding value(s) for the
unknown that make the equation true

Add, subtract, multiply, divide, raise to powers,
take roots, find least common denominators to
isolate the unknown
Example 1: solve for x
3x  22  7 x  2
Example 2: solve for t
S  P  P r t
Example 3
Invest $140,000 with the goal of collecting $10,000
in interest each year. How much should go in risky
account earning 10% interest and how much
should go into safer account earning 5% interest?
Example 3 – continued
interest from 10 %  interest from 5%  10000
Example 4
If profit is linked to number of items sold by the
following equation, where will the company reach
$60,000?
P  80 x  24000
Example 5
When a $980,000 building depreciates in value for
tax purposes, its value, y, after x months of use is
given by:
y  980000 3500x
How many months will it take for the building to
fully depreciate? How many years?
Functions



One quantity depends on another quantity
# of shirts => revenue
Age => Height
Formal definition: A function f is a rule that assigns to each
element x in a set A exactly one element, f(x), in a set B.
( f(x) is read as “ f of x ”)
Algebraic & Graphic
x
Algebraic: f ( x ) 
4
3
Graphic: Plot points (x, f(x)) in the two dimensional plane
f(x)
x
42
-2
f(x) 41
21
2
-21
4
6
8
x
5
9
-4
1
42
-3
27
5
Example 1
Evaluate the function at the indicated values.
f ( x)  x 2  3
f (0), f ( 2), f ( 2 ), f  x  1, f  x 
Domain
The set of all inputs for which the function is a real number.
Three restrictions on the domain for any function:
• Cannot divide by zero
• Cannot have negatives inside an even root
• Cannot have zero or negatives inside logarithms
Examples Find the domain for the following functions.
5 x
f ( x)  2
x  36
D:
g ( x)  11  x
D:
Graphs of Functions

Functions in one variable can be represented by a graph.

Each ordered pair (x, f(x)) that makes the equation true is a
point on the graph.

Graph function by plotting points and then connecting the
points with smooth curves.
Example
f ( x)  4  x
2
Create a table of points:
x
-3
-2
-1
0
y
6
y  f (x)
1
-1
-6
1
x
Domain/Range from Graph
Look at graph to determine domain(inputs) and range (outputs).
f(x)
Domain:
2
-2
2
-2
4
x
Range:
Combining Functions



Take simple functions and combine for more complicated ones
Arithmetic - add, subtract, multiply, divide
Composition – evaluate one function inside another
Given the functions:
f ( x) 
x  5 and g ( x)  x 2
( f  g )( x) 
Domain:
( f  g )( x) 
Domain:
( fg )( x) 
Domain:
f
 (x) 
g
Domain:
Composition
Evaluating one function using another function.
( f  g )( x)  f ( g ( x))
g ( x) is the input for the function, f(x).
Find the composition function:
( f o g )( x)
f ( x)  x  1 and g(x)  x  1
2
Linear Functions
Linear functions also known as lines.
 Each line is defined by: intercepts and slope
 Slope is the change in y over the change in x
 rise over run

Slope
y
(5,6)
(1,3)
x
Forms of Line
General equation:
Ax + By + C = 0
Slope-intercept equation: y  mx  b
slope = m, y-intercept = b
Point-slope equation:
slope = m, point =
y  y1  m( x  x1 )
( x1 , y1 )
Example 1
Given two points, (-2, 9) and (4, 1), on a line,
find the equation of the line.
9
-2
4
Example 2
The U.S. population(in millions) can be described as a
function of time where the independent variable is the
number of years past 1990 with: p (t )  3t  250
Find p(25) and explain what it means.
Graph the function.
750
500
10
20
Example 3
Suppose the cost of a building is $960,000 and a
company wants to use a straight-line depreciation
schedule for 240 months. Write the equation for this
depreciation schedule. y = value of building, x = months
Systems of Linear Equations



A set of equations involving the same variables
A solution is a collection of values that makes each equation
true.
Solving a system = finding all solutions
5 x  3 y  4

 x  3y  2
Substitution Method



Pick one equation and solve for one variable in terms of the other.
Substitute that expression for the variable in the other equation.
Solve the new equation for the single variable and use that value
to find the value of the remaining variable.
5 x  3 y  4

 x  3y  2
Elimination Method



Multiply both equations by constants so that one variable has
coefficients that add to zero.
Add the equations together to eliminate that variable.
Solve the new equation for the single variable and use that value to
find the value of the remaining variable.
 x  3y  2

5 x  3 y  4
Equivalent Systems of Linear Equations




Swap the position of two equations
Multiply equation by non-zero constant
Add a multiple of one equation to another equation
Use Left-to-Right Elimination and then Backward Substitution
 x  3y  2

5 x  3 y  4
x  3 y  2

 18 y  6
Example 1
 3x  4 y  6 z  4

 x  y  4z  1
 x  2 y  7 z  0





 x  y  4z  1

 3x  4 y  6 z  4
 x  2 y  7 z  0




Example 2
 x  2y  z  7

 2 x  y  z  3
 x  2 y  3z  1




Example 3
Each serving (1 cup) of milk contains 430 mg of potassium
and 2.5 g of fat. Each serving (100 g) of peanuts contains
690 mg of potassium and 45 g of fat. If a diet needs to
contain 1205 mg of potassium and 27.5 g of fat, then how
much of each food is needed?
x  servings of milk
y  servings of peanuts
1 serving of milk 
2 servings of milk 
10 servings of milk 
Example 3 – continued
fat : (milk fat )  (peanut fat )  27.5

potassium : (milk pot.)  (peanut pot.)  1205



Applications with Linear Functions

Cost, revenue, profit

Marginals for linear functions

Break Even points

Supply and Demand Equilibrium
Cost, Revenue, Profit, Marginals

Cost: C(x) = variable costs + fixed costs

Revenue: R(x) = (price)(# sold)

Profit: P(x) = R(x) – C(x)

Marginals: what would happen if one more
item were produced (for marginal cost) and sold
(for marginal revenue or marginal profit)
Example 1
C ( x)  22 x  60
R( x)  30 x
Find C(50), R(50), P(50) and interpret.
Find all marginals when x = 50 and interpret.
Example 1 – continued
C ( x)  22 x  60
R( x)  30 x
Find all marginals when x = 50 and interpret.
For linear functions, the marginals are the slopes of the lines.
Break Even Points
Companies break even when costs = revenues
or when profit = 0.
Example 2
C ( x)  75 x  1400
R( x)  89 x
Example 3
If P(10) = -150 and P(50) = 450, how many units are needed
to break even if the profit function is linear?
y  y1  m( x  x1 )
The company breaks even by producing and selling

Law of Demand: quantity demanded goes up as
price goes down. Likewise, as price goes up,
quantity demanded goes down.

Law of Supply: quantity supplied goes up as
price goes up. Likewise, as price goes down,
quantity supplied goes down.

Market Equilibrium: where quantity demanded
equals quantity supplied
Example 4
p
Demand:
p  480  3q
Supply:
p  17q  80
q
Quadratic Equations


Equations involving three terms
constant, linear, and square
ax  bx  c  0
2

Take square root, factor or use quadratic formula
x  49
2
( x  3) 2  25
Factoring
Since AB = 0 implies either A=0 or B = 0, then
rewrite the quadratic equation as a product of
linear factors.
x  10 x  11  0
2
Example 1
5x  8x  4
2
Quadratic Formula
If factoring not nice,
remember quadratic formula:
ax  bx  c  0
2
For given quadratic equation, find solutions for x with:
x=
Examples:
x  10 x  11  0
2
x=
x  2x  4  0
2
x=
Application
A rectangular garden is 8 feet longer than it is wide. If its
area is 240 square feet, then what are its dimensions?
Quadratic Functions & Applications
For f ( x)  ax 2  bx  c, the quadratic function :

Graph is a parabola.

Either has a minimum or maximum point.

That point is called a vertex and is
x-value of the vertex
For the general form : f(x)  ax 2  bx  c,
b
the vertex occurs at x 
.
2a
 b
The extreme value (max or min) is f 
.
 2a 
Example 1
g ( x )  x  10 x  29
2
b
x 
2a
Example 2
g ( x )   x  8 x  13
2
b
x 
2a
Applications
Example 3
Find the break-even point for the given cost and revenue functions.
1 2
C ( x )  3600  25 x  x
2
1 

R ( x)  175  x  x
2 

Company breaks even if it produces and sells
Example 4
Find the maximum revenue for the revenue function given.
R ( x)  1600 x  x
2
R (x)
x
Must sell
units in order to maximize revenue.
Maximum revenue is $
Example 5
Find max revenue where the demand for a product is given.
p  20  x
R (x)
x
Must sell
units in order to maximize revenue.
Maximum revenue is
Example 6
Find the equilibrium point for the given demand and supply functions.
supply : 4 p  q  42
Equilibrium point:
demand : ( p  2)q  2100
Rational Functions
p( x)
f ( x) 
is a rational function when :
q( x)
p(x) and q(x) are polynomials, with
p ( x)  a n x  a n 1 x
n
q ( x )  bm x
m
n 1
 bm 1 x
   a1 x  a0
m 1
   b1 x  b0
Main Characteristic: Asymptotes
Asymptotes are lines (horizontal or vertical) that the
function approaches for certain inputs.
Horizontal: for larger and larger values of x
Vertical: for inputs that get closer to a domain restriction,
in this case, a value that causes division by zero.
Asymptotes
Horizontal: y = k is a horizontal asymptote when n < = m.
p ( x) a n x n ...
f ( x) 

q ( x) bm x m ...
Vertical: x = c is a vertical asymptote when p(c) does not
equal 0 but q(c) does equal 0.
p (c) non  zero
f (c ) 

q (c )
0
f (c)   (or  ) on either side of input c
Example 1
4x  3
f ( x) 
x2
Create a table of points:
x
f(x)
0
-1.5
1
-7
1.5
-18
1.9
-106
2.5
26
3
15
10
5.375
20
4.611111
50
4.229167
100
4.112245
Asymptotes:
f(x)
x
Example 2
Find a few points:
x
f(x)
-1
-1
0
-6
2
20
3
15
x 2  5x  6
f ( x) 
x 1
Asymptotes:
f(x)
x
Example 3
If the cost function for producing x items is given, describe the
associated average cost function.
C ( x)  4000  47 x
Asymptotes:
x