1 Prerequisites: conditional expectation, stopping time
... Prove that ∀t and ∀Y ∈ L (Ω, Ft , P ), EP [Y Zt /Fs ] = Zs EQ [Y /Fs ]. Indication: compute ∀A ∈ Fs , the expectations EP [1A Y Zt ] and EP [1A Zs EQ [Y /Fs ]]. 2. Let be T ≥ 0, Z ∈ M(IP) and Q = ZT IP, 0 ≤ s ≤ t ≤ T and a Ft −measurable random ...
... Prove that ∀t and ∀Y ∈ L (Ω, Ft , P ), EP [Y Zt /Fs ] = Zs EQ [Y /Fs ]. Indication: compute ∀A ∈ Fs , the expectations EP [1A Y Zt ] and EP [1A Zs EQ [Y /Fs ]]. 2. Let be T ≥ 0, Z ∈ M(IP) and Q = ZT IP, 0 ≤ s ≤ t ≤ T and a Ft −measurable random ...
RAMSEY RESULTS INVOLVING THE FIBONACCI NUMBERS 1
... note that the last six gi ’s can be summands of no xj+1 − xj other than possibly xt − xt−1 . Therefore, since the sequence {gi } has 8n + 5 terms, it follows that t − 1 ≤ (8n + 5) − 5(n + 1) = 3n + 3. Now assume x1 6= 1. Then g1 does not appear as a summand in any xj+1 − xj . Also (as in the argumen ...
... note that the last six gi ’s can be summands of no xj+1 − xj other than possibly xt − xt−1 . Therefore, since the sequence {gi } has 8n + 5 terms, it follows that t − 1 ≤ (8n + 5) − 5(n + 1) = 3n + 3. Now assume x1 6= 1. Then g1 does not appear as a summand in any xj+1 − xj . Also (as in the argumen ...
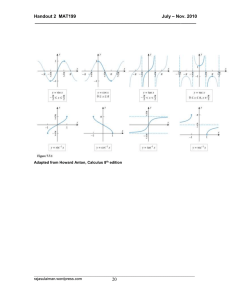
Is it CRITICAL to go to EXTREMES?
... b) Evaluate the 2nd derivative at each critical number to identify and label the relative/local extrema c) If the 2nd derivative at a critical number is positive then it is a relative minimum. d) If the 2nd derivative at a critical number is negative, then it is a relative maximum. e) If the 2nd der ...
... b) Evaluate the 2nd derivative at each critical number to identify and label the relative/local extrema c) If the 2nd derivative at a critical number is positive then it is a relative minimum. d) If the 2nd derivative at a critical number is negative, then it is a relative maximum. e) If the 2nd der ...
Lecture Notes on Elements of Discrete Mathematics: Sets, Functions
... It is clear that the graph of any function from A to B is a subset of A × B. It is sometimes convenient to talk about a function and its graph as if it were the same thing. For instance, instead of writing f (n) = 2n + 1, we can write: f = {h0, 1i, h1, 3i, h2, 5i, . . . }. This convention allows us ...
... It is clear that the graph of any function from A to B is a subset of A × B. It is sometimes convenient to talk about a function and its graph as if it were the same thing. For instance, instead of writing f (n) = 2n + 1, we can write: f = {h0, 1i, h1, 3i, h2, 5i, . . . }. This convention allows us ...
Calculus I: Section 1.3 Intuitive Limits
... and say, “The limit of f (x) as x approaches a equals L,” if we can make the values of f (x) arbitrarily close to L by taking x to be sufficiently close to a on either side of a but not equal to a. This says that the values of f (x) tend to come closer to L as x comes closer and closer to a from eit ...
... and say, “The limit of f (x) as x approaches a equals L,” if we can make the values of f (x) arbitrarily close to L by taking x to be sufficiently close to a on either side of a but not equal to a. This says that the values of f (x) tend to come closer to L as x comes closer and closer to a from eit ...
Multidimensional Calculus. Lectures content. Week 10 22. Tests for
... Definition. Let {fk }k≥n0 , f be functions on a set M . We say that {fk } converges uniformly to f on M , denoted fk → →f , if ∀ε > 0∃N0 ∈ IN such that ∀k ≥ N0 ∀x ∈ M : |f (x) − fk (x)| < ε. Theorem. Let fk → →f on M . (i) If all fk are continuous on M , then also f is continuous there. (ii) If all ...
... Definition. Let {fk }k≥n0 , f be functions on a set M . We say that {fk } converges uniformly to f on M , denoted fk → →f , if ∀ε > 0∃N0 ∈ IN such that ∀k ≥ N0 ∀x ∈ M : |f (x) − fk (x)| < ε. Theorem. Let fk → →f on M . (i) If all fk are continuous on M , then also f is continuous there. (ii) If all ...
Fundamental theorem of calculus
The fundamental theorem of calculus is a theorem that links the concept of the derivative of a function with the concept of the function's integral.The first part of the theorem, sometimes called the first fundamental theorem of calculus, is that the definite integration of a function is related to its antiderivative, and can be reversed by differentiation. This part of the theorem is also important because it guarantees the existence of antiderivatives for continuous functions.The second part of the theorem, sometimes called the second fundamental theorem of calculus, is that the definite integral of a function can be computed by using any one of its infinitely-many antiderivatives. This part of the theorem has key practical applications because it markedly simplifies the computation of definite integrals.