Hand-book on STATISTICAL DISTRIBUTIONS for
... Internal Report SUF–PFY/96–01 Stockholm, 11 December 1996 1st revision, 31 October 1998 last modification 10 September 2007 ...
... Internal Report SUF–PFY/96–01 Stockholm, 11 December 1996 1st revision, 31 October 1998 last modification 10 September 2007 ...
Products of random variables and the first digit phenomenon
... Her is some other notation used in this article: the natural logarithm is denoted by log; for any real x and any integer h, we set eh (x) = exp(2iπhx) where i2 = −1; the symbol {x} stands for the fractional part of a real x; we write Z+ for the set of positive integers; the standard abbreviations a. ...
... Her is some other notation used in this article: the natural logarithm is denoted by log; for any real x and any integer h, we set eh (x) = exp(2iπhx) where i2 = −1; the symbol {x} stands for the fractional part of a real x; we write Z+ for the set of positive integers; the standard abbreviations a. ...
Applications of the Law of Large Numbers in Logistics
... One of the most remarkable theories in probability and statistics is the law of large numbers. Law of large numbers describes the behavior of random phenomena when they are reiterated infinitely or in very large trials. It has been ascertained that determinist phenomena have a very small part in sur ...
... One of the most remarkable theories in probability and statistics is the law of large numbers. Law of large numbers describes the behavior of random phenomena when they are reiterated infinitely or in very large trials. It has been ascertained that determinist phenomena have a very small part in sur ...
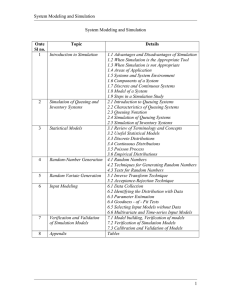
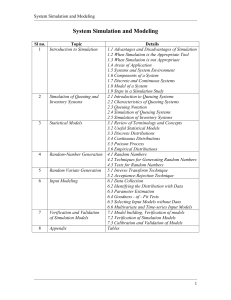
Notes of SMS
... system. It is further classified as static and dynamic models. Static Mathematical Model gives the relationship between the system attributes when the system is in equilibrium. For example in market model there is balance between supply and demand for commodity and both factors depend upon price. Dy ...
... system. It is further classified as static and dynamic models. Static Mathematical Model gives the relationship between the system attributes when the system is in equilibrium. For example in market model there is balance between supply and demand for commodity and both factors depend upon price. Dy ...
Sl no - Sharada Vikas Trust
... system. It is further classified as static and dynamic models. Static Mathematical Model gives the relationship between the system attributes when the system is in equilibrium. For example in market model there is balance between supply and demand for commodity and both factors depend upon price. Dy ...
... system. It is further classified as static and dynamic models. Static Mathematical Model gives the relationship between the system attributes when the system is in equilibrium. For example in market model there is balance between supply and demand for commodity and both factors depend upon price. Dy ...
Chapter 3: Basic Monte Carlo Methods
... computer generated pseudo random numbers have become more and more like independent random variables as the knowledge of these generators grows, the main limit theorems in probability such as the law of large numbers and the central limit theorem still do not have versions which directly apply to de ...
... computer generated pseudo random numbers have become more and more like independent random variables as the knowledge of these generators grows, the main limit theorems in probability such as the law of large numbers and the central limit theorem still do not have versions which directly apply to de ...
Hidden Periodicity and Chaos in the Sequence of Prime Numbers
... also another crucial advantage. If the noise corrupting the gaps sequence has a multiplicative nature, then for the logarithmic gaps this noise will be transformed into an additive one. It is well known that the additive noises can be much readily separated from the signal than the multiplicative on ...
... also another crucial advantage. If the noise corrupting the gaps sequence has a multiplicative nature, then for the logarithmic gaps this noise will be transformed into an additive one. It is well known that the additive noises can be much readily separated from the signal than the multiplicative on ...
Approximation of partial sums of independent random variables Let
... . Since the distribution function of the sum of N independent, identically distributed random variables with expectation zero and variance 1 can be well approximated by the normal distribution function with expectation zero and variance N , and also a good large deviation type result is known about ...
... . Since the distribution function of the sum of N independent, identically distributed random variables with expectation zero and variance 1 can be well approximated by the normal distribution function with expectation zero and variance N , and also a good large deviation type result is known about ...
Week 2
... interest, population growth and radioactive decay. To work effectively with exponential functions, we need to know the rules of exponents. ...
... interest, population growth and radioactive decay. To work effectively with exponential functions, we need to know the rules of exponents. ...
Bernoulli trial
... standardized random variable · the overall shape of the probability distribution function is of most importance · for different values of the mean, the distribution will be “centered” at a different value · for different values of the variance, the distribution will be “stretched” differently · mean ...
... standardized random variable · the overall shape of the probability distribution function is of most importance · for different values of the mean, the distribution will be “centered” at a different value · for different values of the variance, the distribution will be “stretched” differently · mean ...
portable document (.pdf) format
... Although the multivariate Poisson distribution is one of the most well known and important multivariate discrete distributions, it has not found many practical applications apart from the special case of the bivariate Poisson distribution. The main reason for this is the awkward probability functio ...
... Although the multivariate Poisson distribution is one of the most well known and important multivariate discrete distributions, it has not found many practical applications apart from the special case of the bivariate Poisson distribution. The main reason for this is the awkward probability functio ...
Logarithmic Transformation-Based Gamma Random Number
... then T = V /U has density h(t)/Mh . Hence to generate random numbers from the distribution with density h(t)/Mh , we generate a random point (U, V ) uniformly over the ROU region C, often using rejection sampling, and then compute the ratio T = V /U as the output. Cheng and Feast (1980) used the ROU ...
... then T = V /U has density h(t)/Mh . Hence to generate random numbers from the distribution with density h(t)/Mh , we generate a random point (U, V ) uniformly over the ROU region C, often using rejection sampling, and then compute the ratio T = V /U as the output. Cheng and Feast (1980) used the ROU ...
Chapter 3 Gambling, random walks and the Central Limit Theorem
... We are now ready to present our gambler with a mathematically sound advice: yes, it is possible to exploit large mean values present in this game and win a lot. You just need to play this game at least six hundred trillion times. Oh and if you plan to start playing each game with a pound, do not for ...
... We are now ready to present our gambler with a mathematically sound advice: yes, it is possible to exploit large mean values present in this game and win a lot. You just need to play this game at least six hundred trillion times. Oh and if you plan to start playing each game with a pound, do not for ...
On Buffon Machines and Numbers - Algorithms Project
... Flajolet, Louchard, and Schaeffer [7] and Flajolet, Fusy, and Pivoteau [9]. The current implementations relie on real number computations, and they require generating distributions such as geometric, Poisson, or logarithmic, with various ranges of parameters—since the objects ultimately produced are ...
... Flajolet, Louchard, and Schaeffer [7] and Flajolet, Fusy, and Pivoteau [9]. The current implementations relie on real number computations, and they require generating distributions such as geometric, Poisson, or logarithmic, with various ranges of parameters—since the objects ultimately produced are ...
Characteristic functions and the central limit theorem
... we need a better way to deal with sequences of random variables. It is natural to ask, “if we have a sequence of random variables X1 , X2 , . . . such that their characteristic function converge, then do their distributions also converge?” The problem is that the limit of characteristic functions ma ...
... we need a better way to deal with sequences of random variables. It is natural to ask, “if we have a sequence of random variables X1 , X2 , . . . such that their characteristic function converge, then do their distributions also converge?” The problem is that the limit of characteristic functions ma ...
Lecture notes for Section 9.2 (Exponential Functions)
... Big Idea: The exponential function is a base raised to a power that is a variable. Big Skill: You should be able to graph an exponential function, solve basic exponential equations, and use exponential function models. Definition: Exponential Function An exponential function is a function of the for ...
... Big Idea: The exponential function is a base raised to a power that is a variable. Big Skill: You should be able to graph an exponential function, solve basic exponential equations, and use exponential function models. Definition: Exponential Function An exponential function is a function of the for ...