ON ADDITIVE ARITHMETICAL FUNCTIONS AND APPLICATIONS
... Additive and multiplicative functions are thus completely determined if one knows their values for all powers of primes p" . Examples for additive functions are log n, v(n) (the number of distinct prime factors of n) ; examples for multiplicative functions are n, Euler's function q?(n), and b(n) (th ...
... Additive and multiplicative functions are thus completely determined if one knows their values for all powers of primes p" . Examples for additive functions are log n, v(n) (the number of distinct prime factors of n) ; examples for multiplicative functions are n, Euler's function q?(n), and b(n) (th ...
Csorgo, Sandor and Simon, Gordon; (1994).A Strong Law of Large Numbers for Trimmed Sums, with Applications to Generalized St. Petersburg Games."
... is provided by the classical St. Petersburg game, a generalized version of which is discussed in Section 3. Feller (1945, cf. also Section XA of 1968a) used this game to illustrate a weak law in the spirit of (1.12), thereby inaugurating a genuinely mathematical phase in the history of the St. Peter ...
... is provided by the classical St. Petersburg game, a generalized version of which is discussed in Section 3. Feller (1945, cf. also Section XA of 1968a) used this game to illustrate a weak law in the spirit of (1.12), thereby inaugurating a genuinely mathematical phase in the history of the St. Peter ...
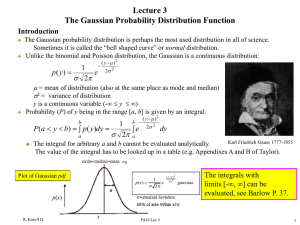
Gaussian Probability Distribution
... Let Y1, Y2,...Yn be an infinite sequence of independent random variables each with the same probability distribution. Suppose that the mean () and variance (2) of this distribution are both finite. For any numbers a and b: Y1 Y2 ...Yn n 1 b 12 y 2 lim Pa b dy e 2 a n ...
... Let Y1, Y2,...Yn be an infinite sequence of independent random variables each with the same probability distribution. Suppose that the mean () and variance (2) of this distribution are both finite. For any numbers a and b: Y1 Y2 ...Yn n 1 b 12 y 2 lim Pa b dy e 2 a n ...
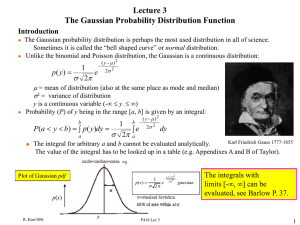
Gaussian Probability Distribution
... Let Y1, Y2,...Yn be an infinite sequence of independent random variables each with the same probability distribution. Suppose that the mean () and variance (2) of this distribution are both finite. For any numbers a and b: Y1 Y2 ...Yn n 1 b 12 y 2 lim Pa b dy e 2 a n ...
... Let Y1, Y2,...Yn be an infinite sequence of independent random variables each with the same probability distribution. Suppose that the mean () and variance (2) of this distribution are both finite. For any numbers a and b: Y1 Y2 ...Yn n 1 b 12 y 2 lim Pa b dy e 2 a n ...
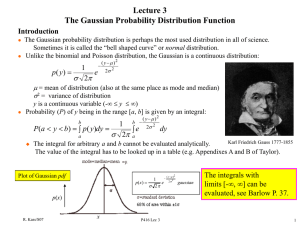
Gaussian Probability Distribution
... u Let Y1, Y2,...Yn be an infinite sequence of independent random variables each with the same probability distribution. u Suppose that the mean () and variance (2) of this distribution are both finite. For any numbers a and b: Actually, the Y’s can Y1 Y2 ...Yn n 1 b 12 y 2 lim Pa ...
... u Let Y1, Y2,...Yn be an infinite sequence of independent random variables each with the same probability distribution. u Suppose that the mean () and variance (2) of this distribution are both finite. For any numbers a and b: Actually, the Y’s can Y1 Y2 ...Yn n 1 b 12 y 2 lim Pa ...
Solution - Statistics
... Statistics 620 Midterm exam, Fall 2013 1. Richard catches trout according to a Poisson process with rate 0.1 minute−1 . Suppose that the trout weigh an average of 4 pounds with a standard deviation of 2 pounds. Find expressions for the mean and standard deviation of the total weight of fish he catch ...
... Statistics 620 Midterm exam, Fall 2013 1. Richard catches trout according to a Poisson process with rate 0.1 minute−1 . Suppose that the trout weigh an average of 4 pounds with a standard deviation of 2 pounds. Find expressions for the mean and standard deviation of the total weight of fish he catch ...
Generating Random Numbers
... no closed-form solution. We can approximate N(x) using a method after Abramowitz and Stegun, as shown in this chart. This approximation produces values of N(x) which are good to within +/_ 4.5x10-4 when modeling a normal distribution with zero mean and unit sigma. You can then convert these normal d ...
... no closed-form solution. We can approximate N(x) using a method after Abramowitz and Stegun, as shown in this chart. This approximation produces values of N(x) which are good to within +/_ 4.5x10-4 when modeling a normal distribution with zero mean and unit sigma. You can then convert these normal d ...
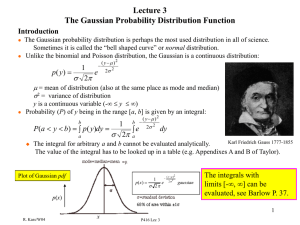
Gaussian Probability Distribution
... Let Y1, Y2,...Yn be an infinite sequence of independent random variables each with the same probability distribution. Suppose that the mean () and variance (2) of this distribution are both finite. For any numbers a and b: Actually, the Y’s can Y1 Y2 ...Yn n 1 b 12 y 2 lim Pa b ...
... Let Y1, Y2,...Yn be an infinite sequence of independent random variables each with the same probability distribution. Suppose that the mean () and variance (2) of this distribution are both finite. For any numbers a and b: Actually, the Y’s can Y1 Y2 ...Yn n 1 b 12 y 2 lim Pa b ...
Section 8.2 Markov and Chebyshev Inequalities and the Weak Law
... EXAMPLE: An astronomer is measuring the distance to a star. Because of different errors, each measurement will not be precisely correct, but merely an estimate. He will therefore make a series of measurements and use the average as his estimate of the distance. He believes his measurements are indep ...
... EXAMPLE: An astronomer is measuring the distance to a star. Because of different errors, each measurement will not be precisely correct, but merely an estimate. He will therefore make a series of measurements and use the average as his estimate of the distance. He believes his measurements are indep ...
Sect. 1.5: Probability Distribution for Large N
... • If X= # of counts per second, then the Poisson probability that X = k (a particular count) is: p( X k ) l ...
... • If X= # of counts per second, then the Poisson probability that X = k (a particular count) is: p( X k ) l ...
Lecture08
... a) Motivation i) As cloth comes off an industrial loom, it occasionally has noticeable flaws. Suppose that a particular loom, producing cloth at a fixed standard width, produces, on average, one such flaw per linear foot (based on past studies of the quality of fabric from the loom). This means that ...
... a) Motivation i) As cloth comes off an industrial loom, it occasionally has noticeable flaws. Suppose that a particular loom, producing cloth at a fixed standard width, produces, on average, one such flaw per linear foot (based on past studies of the quality of fabric from the loom). This means that ...
Sect. 1.5: Probability Distribution for Large N
... • If X= # of counts per second, then the Poisson probability that X = k (a particular count) is: p( X k ) l ...
... • If X= # of counts per second, then the Poisson probability that X = k (a particular count) is: p( X k ) l ...
CONVERGENCE IN DISTRIBUTION !F)!F)!F)!F)!F)!F)!F)!F)!F)!F)!F)!F
... Now assume that { Xn } M. For any x < M we have { P[ Xn x ] } 0, and for any x > M (say x = M + ) we have { P[ Xn M + ] } 1. If these statements are converted to their equivalents in terms of cumulative distribution functions, then we d ...
... Now assume that { Xn } M. For any x < M we have { P[ Xn x ] } 0, and for any x > M (say x = M + ) we have { P[ Xn M + ] } 1. If these statements are converted to their equivalents in terms of cumulative distribution functions, then we d ...