Example 1: A fair die is thrown
... roll two, three? It’s best to make an organized list or a table. Example 5: Two fair dice are thrown. Find the probability that the total of the scores on the two dice is six. First, list the possible outcomes (i.e. the ________________________). How many will there be? _______ . There are two possi ...
... roll two, three? It’s best to make an organized list or a table. Example 5: Two fair dice are thrown. Find the probability that the total of the scores on the two dice is six. First, list the possible outcomes (i.e. the ________________________). How many will there be? _______ . There are two possi ...
Introducing Probability
... Mutually exclusive means the events are disjoint. This means E F = Let's look at a Venn Diagram to see why this is true: E ...
... Mutually exclusive means the events are disjoint. This means E F = Let's look at a Venn Diagram to see why this is true: E ...
chapter 9: introducing probability
... o Classical probability – assume all outcomes are equally likely o Count Buffon (1707-1788) 2048/4040 = .5069 o Karl Pearson (1900) 12,012/24,000 = .5005 o John Kerrich 5067/10,000 = .5067 Random – individual outcomes are uncertain but there is a nonetheless regular distribution of outcomes in lar ...
... o Classical probability – assume all outcomes are equally likely o Count Buffon (1707-1788) 2048/4040 = .5069 o Karl Pearson (1900) 12,012/24,000 = .5005 o John Kerrich 5067/10,000 = .5067 Random – individual outcomes are uncertain but there is a nonetheless regular distribution of outcomes in lar ...
10.8 Geometric Probability - Fay's Mathematics [licensed
... • Definition of Probability – the likelihood of an event occurring. • Usually written P(event) • So if we’re talking about putting all names in hat and pulling one out, the probability or likelihood of my name being pulled out would be written P(Mr. Fay). • Then how would we determine the numerical ...
... • Definition of Probability – the likelihood of an event occurring. • Usually written P(event) • So if we’re talking about putting all names in hat and pulling one out, the probability or likelihood of my name being pulled out would be written P(Mr. Fay). • Then how would we determine the numerical ...
Geometry: Statistics 12.1 A probability experiment is Any possible
... I t would certainly be nice to know in advance how many outcomes we should expect in our sample space. Multiplication Principle: If we can do one task n1 number of ways and a second task n2 number of ways, then both n1 n2 ways. tasks together can be done in _______ ...
... I t would certainly be nice to know in advance how many outcomes we should expect in our sample space. Multiplication Principle: If we can do one task n1 number of ways and a second task n2 number of ways, then both n1 n2 ways. tasks together can be done in _______ ...
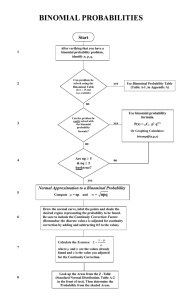
BINOMIAL PROBABILITIES
... Draw the normal curve, label the points and shade the desired region representing the probability to be found. Be sure to include the Continuity Correction Factor. (Remember the discrete value x is adjusted for continuity correction by adding and subtracting 0.5 to the value). ...
... Draw the normal curve, label the points and shade the desired region representing the probability to be found. Be sure to include the Continuity Correction Factor. (Remember the discrete value x is adjusted for continuity correction by adding and subtracting 0.5 to the value). ...
Previous syllabus - Rutgers Business School
... Office Hours: W 1:00-3:00 p.m., or by appointment. Textbook: Introduction to Probability Theory (1971), by P. G. Hoel, S. C. Port, and C. J. Stone, Houghton Mifflin Company: Boston, MA. ISBN: 0-395-04636-x. Examinations: There will be two exams and a comprehensive final exam. Make-up exams will be g ...
... Office Hours: W 1:00-3:00 p.m., or by appointment. Textbook: Introduction to Probability Theory (1971), by P. G. Hoel, S. C. Port, and C. J. Stone, Houghton Mifflin Company: Boston, MA. ISBN: 0-395-04636-x. Examinations: There will be two exams and a comprehensive final exam. Make-up exams will be g ...
B i P b bilit Basic Probability Theory
... • Flipping a coin or choosing a card from a deck at random are both repeatcal p experiments. p • Example 3: • Trial: flipping three coins • Still two possible outcomes: heads or tails • e.g. first=H, second=T, third=T (HTT) • event: set of results e.g. two tails and one head (A = HTT, THT, TTH) ...
... • Flipping a coin or choosing a card from a deck at random are both repeatcal p experiments. p • Example 3: • Trial: flipping three coins • Still two possible outcomes: heads or tails • e.g. first=H, second=T, third=T (HTT) • event: set of results e.g. two tails and one head (A = HTT, THT, TTH) ...
0.5 – Probability
... : The measure of how likely an event is to occur. Each possible result of a probability experiment or situation is an ...
... : The measure of how likely an event is to occur. Each possible result of a probability experiment or situation is an ...
7501 (Probability and Statistics)
... MATH1402. Some basic knowledge of probability is essential, as covered in MATH1301 or the post-examination course on Probability. Dr R Chandler Dr I Strouthos ...
... MATH1402. Some basic knowledge of probability is essential, as covered in MATH1301 or the post-examination course on Probability. Dr R Chandler Dr I Strouthos ...
CCGPS Advanced Algebra
... What is the likelihood that a focus group of 10 women chosen to try the product contains 2 women who did not see a reduction in wrinkles? 6. What is the probability of a fair coin landing heads-up 3 times in 6 tosses? 7. What is the likelihood of a fair six-sided die coming up with a number greater ...
... What is the likelihood that a focus group of 10 women chosen to try the product contains 2 women who did not see a reduction in wrinkles? 6. What is the probability of a fair coin landing heads-up 3 times in 6 tosses? 7. What is the likelihood of a fair six-sided die coming up with a number greater ...
Chapter 5 Objectives and Assignments
... Objectives and Assignments Objectives Students will be able to: 1. Interpret probability as a long-run relative frequency in context. 2. Use simulation to model chance behavior. 3. Describe a probability model for a chance process. 4. Use basic probability rules, including the complement rule and th ...
... Objectives and Assignments Objectives Students will be able to: 1. Interpret probability as a long-run relative frequency in context. 2. Use simulation to model chance behavior. 3. Describe a probability model for a chance process. 4. Use basic probability rules, including the complement rule and th ...
Sampling Theory • sample space set of all possible outcomes of a
... set of all possible outcomes of a chance experiment • event set of one or more outcomes from the sample space • probability model method for assigning probabilities to the outcomes in a sample space • disjoint events events which have no outcomes in common, i.e., can never occur simultaneously Rules ...
... set of all possible outcomes of a chance experiment • event set of one or more outcomes from the sample space • probability model method for assigning probabilities to the outcomes in a sample space • disjoint events events which have no outcomes in common, i.e., can never occur simultaneously Rules ...