Lecture 14 1 Entanglement and Spin
... Well, we know that an electron has a magnetic dipole moment that is related to its spin. Magnetic dipole moments come up classically when you have current loops, so conceptually we can think of electrons as little current loops that generate dipolar magnetic fields. But if one electron generates a m ...
... Well, we know that an electron has a magnetic dipole moment that is related to its spin. Magnetic dipole moments come up classically when you have current loops, so conceptually we can think of electrons as little current loops that generate dipolar magnetic fields. But if one electron generates a m ...
The Interaction of Radiation and Matter: Quantum
... defines or generates a two-dimensional Taylor expansion when it acts on a function of and . In particular, if we take the "phase space" representation of the ground or vacuum state as the product of two Gaussians (see Equations [ I-10a ] and [ I-29 ]), then representation -- i.e. ...
... defines or generates a two-dimensional Taylor expansion when it acts on a function of and . In particular, if we take the "phase space" representation of the ground or vacuum state as the product of two Gaussians (see Equations [ I-10a ] and [ I-29 ]), then representation -- i.e. ...
Quantum Mechanics
... 'colors'. Lets not forget the gluons, the even smaller particles that hold this mess together when they collect and form glueballs. The quantum model of the atom is much more complex than the traditional model. The world of subatomic particles is a very bizarre one, filled with quantum probabilities ...
... 'colors'. Lets not forget the gluons, the even smaller particles that hold this mess together when they collect and form glueballs. The quantum model of the atom is much more complex than the traditional model. The world of subatomic particles is a very bizarre one, filled with quantum probabilities ...
Fulltext
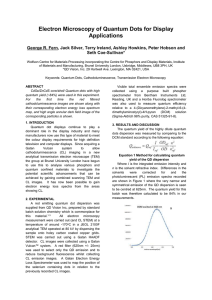
... the QD ensemble and figure 2b shows for the first time by us the red light filtered CL image. There is a clear distribution of sizes present, see regions shown inside the triangles. The larger particles show CL activity (e.g. region shown by the arrow in a and b and circled in c) but the smaller par ...
... the QD ensemble and figure 2b shows for the first time by us the red light filtered CL image. There is a clear distribution of sizes present, see regions shown inside the triangles. The larger particles show CL activity (e.g. region shown by the arrow in a and b and circled in c) but the smaller par ...
What is quantum chaos?
... parameter scaling theory we propose an alternative characterization of this universality class. It is also identified the universality class associated to the metal-insulator transition. In low dimensions it is characterized by classical superdiffusion. In higher dimensions it has in general a quant ...
... parameter scaling theory we propose an alternative characterization of this universality class. It is also identified the universality class associated to the metal-insulator transition. In low dimensions it is characterized by classical superdiffusion. In higher dimensions it has in general a quant ...
Another version - Scott Aaronson
... B is maximally entangled with the last qubit of R. But in order to see that B and R are even classically correlated, one would need to learn xs (a “hardcore bit” of f), and therefore invert f With realistic dynamics, the decoding task seems like it should only be “harder” than in this model case (t ...
... B is maximally entangled with the last qubit of R. But in order to see that B and R are even classically correlated, one would need to learn xs (a “hardcore bit” of f), and therefore invert f With realistic dynamics, the decoding task seems like it should only be “harder” than in this model case (t ...
Chapter 1 Review of Quantum Mechanics
... which correspond to different states of the particle’s motion. Therefore, people sometime use these discrete set of quantum numbers to characterize state of the particle’s motion. A state function such as Φk (r) can not be measured directly. It has a meaning of probability : its modular |Φk (r)|2 gi ...
... which correspond to different states of the particle’s motion. Therefore, people sometime use these discrete set of quantum numbers to characterize state of the particle’s motion. A state function such as Φk (r) can not be measured directly. It has a meaning of probability : its modular |Φk (r)|2 gi ...
Homework 3: Due in class on Monday, Oct 21st, 2013
... states for ~h = 0, which is 2 for S = 1/2. Initially, the system is prepared in a state having a definite projection of the spin on the field, |N i, where N measures the component of the spin along the field. (In the case of spin-1/2 we considered the |+i state, which corresponds to N = 1/2.) Genera ...
... states for ~h = 0, which is 2 for S = 1/2. Initially, the system is prepared in a state having a definite projection of the spin on the field, |N i, where N measures the component of the spin along the field. (In the case of spin-1/2 we considered the |+i state, which corresponds to N = 1/2.) Genera ...
... Consider the following model of a perfectly smooth cylinder. It is a ring of equally spaced, identical particles, with mass M N so that the mass of the ring is M and its moment of inertia MR2 with R the radius of the ring. Calculate the possible values of the angular momentum. Calculate the energy e ...
... Consider the following model of a perfectly smooth cylinder. It is a ring of equally spaced, identical particles, with mass M N so that the mass of the ring is M and its moment of inertia MR2 with R the radius of the ring. Calculate the possible values of the angular momentum. Calculate the energy e ...
Elements of Dirac Notation
... bra-ket pairs, ket-bra products, and the completeness relation (continuous and discreet). With these few building blocks you can construct all of quantum theory. 2. It is flexible. You can use it to say the same thing in several ways; translate with ease from one language to another. Perhaps the ins ...
... bra-ket pairs, ket-bra products, and the completeness relation (continuous and discreet). With these few building blocks you can construct all of quantum theory. 2. It is flexible. You can use it to say the same thing in several ways; translate with ease from one language to another. Perhaps the ins ...
Erwin Schroedinger, Max Born and Wave Mechanics
... space, or orbitals, where electrons are most likely to be found Describes the probability that an electron can be found in a given region of space at a given time Says where the Electron might be Bohr’s model- electrons move in a circular motion around the nucleus ...
... space, or orbitals, where electrons are most likely to be found Describes the probability that an electron can be found in a given region of space at a given time Says where the Electron might be Bohr’s model- electrons move in a circular motion around the nucleus ...
Ab Initio Predictions for Potential Energy Surfaces for Chemical
... and Y a weighted (bj), so that there a many fewer indices than in normal coupled-cluster theory. This is particularly important as we go to higher amplitudes like T3, where a computational ~n8 procedure can be dramatically reduced. Similarly, the use of frozen natural r can have a similar effect, bu ...
... and Y a weighted (bj), so that there a many fewer indices than in normal coupled-cluster theory. This is particularly important as we go to higher amplitudes like T3, where a computational ~n8 procedure can be dramatically reduced. Similarly, the use of frozen natural r can have a similar effect, bu ...
Do Global Virtual Axionic Gravitons Exist?
... Nevertheless, looking from the present-day theoretical point of view, the model reasoning presented in this paper allows to make use of the hypothetically existing virtual axionic particle-like global gravitons in order to search, ...
... Nevertheless, looking from the present-day theoretical point of view, the model reasoning presented in this paper allows to make use of the hypothetically existing virtual axionic particle-like global gravitons in order to search, ...
Document
... Which of the following phenomena could be explained by classical physics and did not require a quantum hypothesis in order to make theory agree with experiment? ...
... Which of the following phenomena could be explained by classical physics and did not require a quantum hypothesis in order to make theory agree with experiment? ...
Quantum Field Theory - damtp
... At distances shorter than this, there is a high probability that we will detect particleanti-particle pairs swarming around the original particle that we put in. The distance λ is called the Compton wavelength. It is always smaller than the de Broglie wavelength λdB = h/|~p|. If you like, the de Br ...
... At distances shorter than this, there is a high probability that we will detect particleanti-particle pairs swarming around the original particle that we put in. The distance λ is called the Compton wavelength. It is always smaller than the de Broglie wavelength λdB = h/|~p|. If you like, the de Br ...