2.1 - Patterns and Inductive Reasoning.notebook
... sure. You can prove that a conjecture is false by finding one counterexample. A counterexample is an example that shows that a conjecture is false. Ex 5). What is a counterexample for each conjecture? a) If an animal is green, it is a frog. ...
... sure. You can prove that a conjecture is false by finding one counterexample. A counterexample is an example that shows that a conjecture is false. Ex 5). What is a counterexample for each conjecture? a) If an animal is green, it is a frog. ...
Lecture 3 Slides
... Claim: Every natural number is either a Fibonacci number, or can be written as the sum of Fibonacci numbers. ...
... Claim: Every natural number is either a Fibonacci number, or can be written as the sum of Fibonacci numbers. ...
Consecutive Sums
... 1 + 2 + 3 + 4 + 5. HINT: Organizing your work will help you to find patterns. • Find as many patterns as you find. Are there any numbers that cannot be written with consecutive sums? Are some numbers easier to find than others? Write as many generalizations as you can about the patterns you found. • ...
... 1 + 2 + 3 + 4 + 5. HINT: Organizing your work will help you to find patterns. • Find as many patterns as you find. Are there any numbers that cannot be written with consecutive sums? Are some numbers easier to find than others? Write as many generalizations as you can about the patterns you found. • ...
Levan Scott Academy Lesson Plan
... 2-3: Some real-world quantities have a mathematical relationship; the value of one quantity can be found if you know the value of the other quantity. 2-4: Some real-world quantities have a mathematical relationship; the value of one quantity can be found if the value of the other quantity is known. ...
... 2-3: Some real-world quantities have a mathematical relationship; the value of one quantity can be found if you know the value of the other quantity. 2-4: Some real-world quantities have a mathematical relationship; the value of one quantity can be found if the value of the other quantity is known. ...
Description - BGCoder.com
... Start from the first number in the valley (valley[0]) and add the number to the coins collected. Then use the first number in the pattern (pattern[0]) and go to position (0 + pattern[0]) in the valley. Collect the coins from position 0 + pattern [0] and go to position (0 + pattern[0]) + pattern[1]m ...
... Start from the first number in the valley (valley[0]) and add the number to the coins collected. Then use the first number in the pattern (pattern[0]) and go to position (0 + pattern[0]) in the valley. Collect the coins from position 0 + pattern [0] and go to position (0 + pattern[0]) + pattern[1]m ...
Recognise, copy, continue, create and describe repeating patterns
... Teacher draws a simple 2-object pattern (e.g. heart, square). Students asked to draw and continue the pattern on their whiteboard. 7. Teacher draws a more complex pattern (3-4 pictures or shapes). Students asked to draw and continue the pattern on their whiteboard. 8. Students asked to create and re ...
... Teacher draws a simple 2-object pattern (e.g. heart, square). Students asked to draw and continue the pattern on their whiteboard. 7. Teacher draws a more complex pattern (3-4 pictures or shapes). Students asked to draw and continue the pattern on their whiteboard. 8. Students asked to create and re ...
the instructions
... The Powers of 2 is a very compact and useful way to describe numbers in this pattern. It represents how many times we have to multiply 2 to reach the number. The binary branching pattern (shown ...
... The Powers of 2 is a very compact and useful way to describe numbers in this pattern. It represents how many times we have to multiply 2 to reach the number. The binary branching pattern (shown ...
Inductive reasoning- coming to a conclusion by recognizing a
... 5. For any three points in a plane, there are three different lines that contain two of the points. ...
... 5. For any three points in a plane, there are three different lines that contain two of the points. ...
1_7 Patterns and Sequences Notes
... Each month, Eva chooses 3 new DVDs from her DVD club. Eva’s DVDs Position ...
... Each month, Eva chooses 3 new DVDs from her DVD club. Eva’s DVDs Position ...
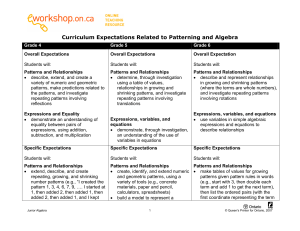
Curriculum Expectations Related to Patterning and
... variety of tools and strategies (e.g., • demonstrate, through investigation, modelling with concrete materials, an understanding of variables as using guess-and-check with and unknown quantities represented by without the aid of a calculator); a letter or other symbol (e.g., 12 = • identify, through ...
... variety of tools and strategies (e.g., • demonstrate, through investigation, modelling with concrete materials, an understanding of variables as using guess-and-check with and unknown quantities represented by without the aid of a calculator); a letter or other symbol (e.g., 12 = • identify, through ...
Conjecture
... We want to know what the next three numbers / terms of this sequence will be as well as the general term of the sequence. Each sequence is a group of numbers that has two very important properties: the terms are listed in a specific order and there is a rule which enables you to continue with the se ...
... We want to know what the next three numbers / terms of this sequence will be as well as the general term of the sequence. Each sequence is a group of numbers that has two very important properties: the terms are listed in a specific order and there is a rule which enables you to continue with the se ...
Content Area: Mathematics Standard: 2. Patterns, Functions, and Algebraic Structures
... Relevance and Application: 1. The use of a pattern of elapsed time helps to set up a schedule. For example, classes are each 50 minutes with 5 minutes between each class. 2. The ability to use patterns allows problem-solving. For example, a rancher needs to know how many shoes to buy for his horses, ...
... Relevance and Application: 1. The use of a pattern of elapsed time helps to set up a schedule. For example, classes are each 50 minutes with 5 minutes between each class. 2. The ability to use patterns allows problem-solving. For example, a rancher needs to know how many shoes to buy for his horses, ...
Learning Area
... Learning Outcome(s) and Assessment Standard(s): Learning Outcome 2: Patterns, Functions and Algebra Assessment Standard: We know this when the learner 8.2.1 Investigates and extends numeric and geometric patterns looking for a relationship or rules, including patterns: represented in physical or dia ...
... Learning Outcome(s) and Assessment Standard(s): Learning Outcome 2: Patterns, Functions and Algebra Assessment Standard: We know this when the learner 8.2.1 Investigates and extends numeric and geometric patterns looking for a relationship or rules, including patterns: represented in physical or dia ...
repeating and growing patterns
... The pattern can have` long or short units. The pattern can include any items such as… numbers, shapes, or colors. ...
... The pattern can have` long or short units. The pattern can include any items such as… numbers, shapes, or colors. ...
deceptive patterns in mathematics
... where a can be any one of the values 2, 3, 4, 5, .…… (in fact, any number for that matter), and it is easy to see that in (4) we have got that infinite number of formulae, since for any such value of a we get 2, 4, 6, 8 when we put n = 1, 2, 3, 4 respectively in (4). The moral of all the discussion ...
... where a can be any one of the values 2, 3, 4, 5, .…… (in fact, any number for that matter), and it is easy to see that in (4) we have got that infinite number of formulae, since for any such value of a we get 2, 4, 6, 8 when we put n = 1, 2, 3, 4 respectively in (4). The moral of all the discussion ...
www.sju.edu/~rhall/Rhythms/poets.pdf
... Hemacandra (and my students) discovered that each number in the sequence on the right hand column is found by adding the two numbers above it. In other words, he found the Fibonacci numbers—half a century before Fibonacci! Singh theorizes that Fibonacci, who was educated in North Africa and came int ...
... Hemacandra (and my students) discovered that each number in the sequence on the right hand column is found by adding the two numbers above it. In other words, he found the Fibonacci numbers—half a century before Fibonacci! Singh theorizes that Fibonacci, who was educated in North Africa and came int ...
Patterns_and_Sequences
... Patterns and sequences We often need to spot a pattern in order to predict what will happen next. In maths, the correct name for a pattern of numbers is called a SEQUENCE. The first number in a SEQUENCE is sometimes called the FIRST TERM; the second is the SECOND TERM and so on. ...
... Patterns and sequences We often need to spot a pattern in order to predict what will happen next. In maths, the correct name for a pattern of numbers is called a SEQUENCE. The first number in a SEQUENCE is sometimes called the FIRST TERM; the second is the SECOND TERM and so on. ...
Park Lakes 5th Grade Science
... pictorial patterns in order to make predictions and solve problems. Students will use patterns to skip by twos, fives and tens. ...
... pictorial patterns in order to make predictions and solve problems. Students will use patterns to skip by twos, fives and tens. ...
Learning Area
... Assessment Standard: We know this when the learner 9.2.1 Investigates, in different ways, a variety of numeric and geometric patterns and relationships by representing and generalising them, and by explaining and justifying the rules that generate them (including patterns found in natural and cultur ...
... Assessment Standard: We know this when the learner 9.2.1 Investigates, in different ways, a variety of numeric and geometric patterns and relationships by representing and generalising them, and by explaining and justifying the rules that generate them (including patterns found in natural and cultur ...
Grade 9 Patterns: number
... Learning Outcome(s) and Assessment Standard(s): Learning Outcome 2: Patterns, Functions and Algebra Assessment Standard: We know this when the learner 9.2.1 Investigates, in different ways, a variety of numeric and geometric patterns and relationships by representing and generalizing them, and by ex ...
... Learning Outcome(s) and Assessment Standard(s): Learning Outcome 2: Patterns, Functions and Algebra Assessment Standard: We know this when the learner 9.2.1 Investigates, in different ways, a variety of numeric and geometric patterns and relationships by representing and generalizing them, and by ex ...
Maths-2011_Leader_Symposium_Algebra_ppt
... Structure (AMPS) generalises across early mathematical concepts, can be reliably measured, and is correlated with mathematical understanding” (Mulligan & Mitchelmore, 2009) ...
... Structure (AMPS) generalises across early mathematical concepts, can be reliably measured, and is correlated with mathematical understanding” (Mulligan & Mitchelmore, 2009) ...
Patterns in nature

Patterns in nature are visible regularities of form found in the natural world. These patterns recur in different contexts and can sometimes be modelled mathematically. Natural patterns include symmetries, trees, spirals, meanders, waves, foams, tessellations, cracks and stripes. Early Greek philosophers studied pattern, with Plato, Pythagoras and Empedocles attempting to explain order in nature. The modern understanding of visible patterns developed gradually over time.In the 19th century, Belgian physicist Joseph Plateau examined soap films, leading him to formulate the concept of a minimal surface. German biologist and artist Ernst Haeckel painted hundreds of marine organisms to emphasise their symmetry. Scottish biologist D'Arcy Thompson pioneered the study of growth patterns in both plants and animals, showing that simple equations could explain spiral growth. In the 20th century, British mathematician Alan Turing predicted mechanisms of morphogenesis which give rise to patterns of spots and stripes. Hungarian biologist Aristid Lindenmayer and French American mathematician Benoît Mandelbrot showed how the mathematics of fractals could create plant growth patterns.Mathematics, physics and chemistry can explain patterns in nature at different levels. Patterns in living things are explained by the biological processes of natural selection and sexual selection. Studies of pattern formation make use of computer models to simulate a wide range of patterns.