Part 18
... mathematical operator that is necessary in order to get the total energy of the system E from the wavefunction ψ. In our particle in a box example, we solved the Schrödinger equation as: ...
... mathematical operator that is necessary in order to get the total energy of the system E from the wavefunction ψ. In our particle in a box example, we solved the Schrödinger equation as: ...
Wissink P640 – Subatomic Physics I Fall 2007 Problem Set # 1
... here as well for the 2π decay, so we must require the two outgoing pions couple to isospin Itot = 1. But the ω, unlike the ρ, is an isospin-0 particle, so the decay ω 0 → π π (for either charged or neutral pions) has I = 0 in the initial state and must have I = 1 in the final state ⇒ can’t proceed. ...
... here as well for the 2π decay, so we must require the two outgoing pions couple to isospin Itot = 1. But the ω, unlike the ρ, is an isospin-0 particle, so the decay ω 0 → π π (for either charged or neutral pions) has I = 0 in the initial state and must have I = 1 in the final state ⇒ can’t proceed. ...
Spatial and Temporal Wave Functions of Photon
... Heisenberg uncertainty relations eq. (4), it follows that the uncertainty in time is t . This means that one cannot specify the time coordinate hence one can consider the wave function of the electron with the frequency in time. The temporal wave function of the electron has the null speed wi ...
... Heisenberg uncertainty relations eq. (4), it follows that the uncertainty in time is t . This means that one cannot specify the time coordinate hence one can consider the wave function of the electron with the frequency in time. The temporal wave function of the electron has the null speed wi ...
Quantum Master Equation of a Particle in a Gas Environment.
... This is the central result of our letter: a quantum master equation of Lindblad form [4] with Lindblad generators v k ; k : , describing the fluctuational-frictional evolution of the Brownian particle's density operator p, valid a t time scales longer than the typical collision time. We shall prove ...
... This is the central result of our letter: a quantum master equation of Lindblad form [4] with Lindblad generators v k ; k : , describing the fluctuational-frictional evolution of the Brownian particle's density operator p, valid a t time scales longer than the typical collision time. We shall prove ...
3. Atomic and molecular structure
... gives the equation in the more familiar form of the particle in a one-dimensional box, which you will see in Chemistry 3730: ...
... gives the equation in the more familiar form of the particle in a one-dimensional box, which you will see in Chemistry 3730: ...
1.5. Angular momentum operators
... 1. BASICS CONCEPTS OF QUANTUM MECHANICS Discussion of the solution: representation of orbitals Some other picture of the p and d orbitals: ...
... 1. BASICS CONCEPTS OF QUANTUM MECHANICS Discussion of the solution: representation of orbitals Some other picture of the p and d orbitals: ...
Methods of Theoretical Physics I (Physics 811)
... Homework: specific assignments and due dates are given on the blackboard; Homework should be turned in in the hardcopy form (electron files will not be accepted) by 5 p.m. on the due date by giving it to the instructor personally or placing it in the instructor's mail box. Homework turned in after t ...
... Homework: specific assignments and due dates are given on the blackboard; Homework should be turned in in the hardcopy form (electron files will not be accepted) by 5 p.m. on the due date by giving it to the instructor personally or placing it in the instructor's mail box. Homework turned in after t ...
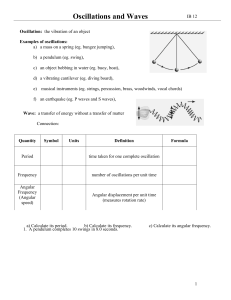
pkt 9 SHM and waves
... provide accurate clocks for microprocessors and to produce and detect sound waves in a medical test known as ultrasound. d) Greenhouse Effect: The natural frequency of oscillation of the molecules of the greenhouse gases (water vapor, carbon dioxide, methane, nitrous oxide) is in the infrared region ...
... provide accurate clocks for microprocessors and to produce and detect sound waves in a medical test known as ultrasound. d) Greenhouse Effect: The natural frequency of oscillation of the molecules of the greenhouse gases (water vapor, carbon dioxide, methane, nitrous oxide) is in the infrared region ...
Schroedinger equation Basic postulates of quantum mechanics
... In general we integrate over the set variables the wave function of the system is defined on, and normalized on. In “space representation” of quantum mechanics we discuss right now this is space coordinates. For example an expectation value of a position of a particle will be: ...
... In general we integrate over the set variables the wave function of the system is defined on, and normalized on. In “space representation” of quantum mechanics we discuss right now this is space coordinates. For example an expectation value of a position of a particle will be: ...
Many-Electron States - cond
... enough: their characteristic traits give them individuality. It has therefore been argued that objects that cannot be distinguished must be identical, as Leibnitz did with his Principle of the Identity of Indiscernibles [1]. We might, however, imagine a replicator that could produce a perfect clone ...
... enough: their characteristic traits give them individuality. It has therefore been argued that objects that cannot be distinguished must be identical, as Leibnitz did with his Principle of the Identity of Indiscernibles [1]. We might, however, imagine a replicator that could produce a perfect clone ...
Free Fields, Harmonic Oscillators, and Identical Bosons
... quantum theory of Maxwell fields F µν (x) is identical to the quantum theory of (any number of) photons — which are massless relativistic particles with two polarizations states (per photon) and obey Bose statistics. Quantization of field theories with non-quadratic Hamiltonians (and hence non-linea ...
... quantum theory of Maxwell fields F µν (x) is identical to the quantum theory of (any number of) photons — which are massless relativistic particles with two polarizations states (per photon) and obey Bose statistics. Quantization of field theories with non-quadratic Hamiltonians (and hence non-linea ...
Quantum mechanics is the theory that we use to describe the
... In 1905, Albert Einstein used the idea of quantised states to explain the photoelectric effect. He explained the observed frequency dependence of the emitted particles by postulating that light energy too comes in tiny discrete bits, or quanta. These discrete light packets, or photons, also come in ...
... In 1905, Albert Einstein used the idea of quantised states to explain the photoelectric effect. He explained the observed frequency dependence of the emitted particles by postulating that light energy too comes in tiny discrete bits, or quanta. These discrete light packets, or photons, also come in ...
here
... • The set of possible instantaneous locations of a classical particle is called its configuration space. This is usually three dimensional Euclidean space R3 . The number of coordinates needed to specify the instantaneous configuration of a system is the number of degrees of freedom. A system consis ...
... • The set of possible instantaneous locations of a classical particle is called its configuration space. This is usually three dimensional Euclidean space R3 . The number of coordinates needed to specify the instantaneous configuration of a system is the number of degrees of freedom. A system consis ...
Relation Between Schrödinger and Polymer Quantum Mechanics
... The only thing possible: approximate the non-existing term by a well defined function that can be quantized and hope for the best. Let us chose the position to be discrete, so p̂ does not exist. With this choice, the kinetic term p̂2/2m has to be approximated, for any potential. How is this done? Th ...
... The only thing possible: approximate the non-existing term by a well defined function that can be quantized and hope for the best. Let us chose the position to be discrete, so p̂ does not exist. With this choice, the kinetic term p̂2/2m has to be approximated, for any potential. How is this done? Th ...
Wave function

A wave function in quantum mechanics describes the quantum state of an isolated system of one or more particles. There is one wave function containing all the information about the entire system, not a separate wave function for each particle in the system. Its interpretation is that of a probability amplitude. Quantities associated with measurements, such as the average momentum of a particle, can be derived from the wave function. It is a central entity in quantum mechanics and is important in all modern theories, like quantum field theory incorporating quantum mechanics, while its interpretation may differ. The most common symbols for a wave function are the Greek letters ψ or Ψ (lower-case and capital psi).For a given system, once a representation corresponding to a maximal set of commuting observables and a suitable coordinate system is chosen, the wave function is a complex-valued function of the system's degrees of freedom corresponding to the chosen representation and coordinate system, continuous as well as discrete. Such a set of observables, by a postulate of quantum mechanics, are Hermitian linear operators on the space of states representing a set of physical observables, like position, momentum and spin that can, in principle, be simultaneously measured with arbitrary precision. Wave functions can be added together and multiplied by complex numbers to form new wave functions, and hence are elements of a vector space. This is the superposition principle of quantum mechanics. This vector space is endowed with an inner product such that it is a complete metric topological space with respect to the metric induced by the inner product. In this way the set of wave functions for a system form a function space that is a Hilbert space. The inner product is a measure of the overlap between physical states and is used in the foundational probabilistic interpretation of quantum mechanics, the Born rule, relating transition probabilities to inner products. The actual space depends on the system's degrees of freedom (hence on the chosen representation and coordinate system) and the exact form of the Hamiltonian entering the equation governing the dynamical behavior. In the non-relativistic case, disregarding spin, this is the Schrödinger equation.The Schrödinger equation determines the allowed wave functions for the system and how they evolve over time. A wave function behaves qualitatively like other waves, such as water waves or waves on a string, because the Schrödinger equation is mathematically a type of wave equation. This explains the name ""wave function"", and gives rise to wave–particle duality. The wave of the wave function, however, is not a wave in physical space; it is a wave in an abstract mathematical ""space"", and in this respect it differs fundamentally from water waves or waves on a string.For a given system, the choice of which relevant degrees of freedom to use are not unique, and correspondingly the domain of the wave function is not unique. It may be taken to be a function of all the position coordinates of the particles over position space, or the momenta of all the particles over momentum space, the two are related by a Fourier transform. These descriptions are the most important, but they are not the only possibilities. Just like in classical mechanics, canonical transformations may be used in the description of a quantum system. Some particles, like electrons and photons, have nonzero spin, and the wave function must include this fundamental property as an intrinsic discrete degree of freedom. In general, for a particle with half-integer spin the wave function is a spinor, for a particle with integer spin the wave function is a tensor. Particles with spin zero are called scalar particles, those with spin 1 vector particles, and more generally for higher integer spin, tensor particles. The terminology derives from how the wave functions transform under a rotation of the coordinate system. No elementary particle with spin 3⁄2 or higher is known, except for the hypothesized spin 2 graviton. Other discrete variables can be included, such as isospin. When a system has internal degrees of freedom, the wave function at each point in the continuous degrees of freedom (e.g. a point in space) assigns a complex number for each possible value of the discrete degrees of freedom (e.g. z-component of spin). These values are often displayed in a column matrix (e.g. a 2 × 1 column vector for a non-relativistic electron with spin 1⁄2).In the Copenhagen interpretation, an interpretation of quantum mechanics, the squared modulus of the wave function, |ψ|2, is a real number interpreted as the probability density of measuring a particle as being at a given place at a given time or having a definite momentum, and possibly having definite values for discrete degrees of freedom. The integral of this quantity, over all the system's degrees of freedom, must be 1 in accordance with the probability interpretation, this general requirement a wave function must satisfy is called the normalization condition. Since the wave function is complex valued, only its relative phase and relative magnitude can be measured. Its value does not in isolation tell anything about the magnitudes or directions of measurable observables; one has to apply quantum operators, whose eigenvalues correspond to sets of possible results of measurements, to the wave function ψ and calculate the statistical distributions for measurable quantities.The unit of measurement for ψ depends on the system, and can be found by dimensional analysis of the normalization condition for the system. For one particle in three dimensions, its units are [length]−3/2, because an integral of |ψ|2 over a region of three-dimensional space is a dimensionless probability.