Quanta and Waves Student booklet II ROR
... individual disturbances produced by each wave at that point. As a consequence of this, waves can pass through one another without being affected in any way. For example if two stones are dropped into a pool of calm water, two sets of circular waves are produced. These two waves pass through each oth ...
... individual disturbances produced by each wave at that point. As a consequence of this, waves can pass through one another without being affected in any way. For example if two stones are dropped into a pool of calm water, two sets of circular waves are produced. These two waves pass through each oth ...
The two-state vector description of a quantum system
... Is this the two-state vector which describes the Universe? No! The backward evolving quantum state is equal to the forward evolving state! Prob(C c) PC c ...
... Is this the two-state vector which describes the Universe? No! The backward evolving quantum state is equal to the forward evolving state! Prob(C c) PC c ...
A Signed Particle Formulation of Non
... In this paper, we introduce a new formulation of quantum mechanics in terms of signed classical field-less particles. This suggested theory is based on a generalization and a novel physical interpretation of the mathematical Wigner Monte Carlo method [8] which is able to simulate the time-dependent ...
... In this paper, we introduce a new formulation of quantum mechanics in terms of signed classical field-less particles. This suggested theory is based on a generalization and a novel physical interpretation of the mathematical Wigner Monte Carlo method [8] which is able to simulate the time-dependent ...
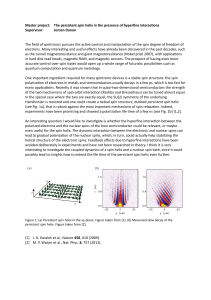
The persistent spin helix in the presence of hyperfine
... in hard disk read heads, magnetic RAM, and magnetic sensors. The prospect of having even more accurate control over spin states would open up a whole range of futuristic possibilities such as quantum computation and quantum metrology. One important ingredient required for many spintronic devices is ...
... in hard disk read heads, magnetic RAM, and magnetic sensors. The prospect of having even more accurate control over spin states would open up a whole range of futuristic possibilities such as quantum computation and quantum metrology. One important ingredient required for many spintronic devices is ...
Introduction Introduction to statistical statistical mechanics
... admissible microstates with density defined as statistical ensemble. ensemble A statistical ensembles are defined and named by the distribution function which characterizes it. The statistical average value have the same meaning as the ensemble average value. An ensemble A bl is i said id to be b ...
... admissible microstates with density defined as statistical ensemble. ensemble A statistical ensembles are defined and named by the distribution function which characterizes it. The statistical average value have the same meaning as the ensemble average value. An ensemble A bl is i said id to be b ...
Chapter 11 Quantum statistics
... manifests itself in the statistical interpretation of the wave function and in the uncertainty relation between qi and pi , which cannot be anymore sharply measured at the same time. The concepts of phase space and phase trajectory have no meaning anymore. ...
... manifests itself in the statistical interpretation of the wave function and in the uncertainty relation between qi and pi , which cannot be anymore sharply measured at the same time. The concepts of phase space and phase trajectory have no meaning anymore. ...
Theoretical Chemistry
... larger molecules. The number of variables there (x,y and z coordinates for each electron and nucleus) is equal to 3*(n+N). This gives even for rather small benzene (C6H6) with 12 nuclei and 42 electrons quite large dimension of 162. Thus, the Schrödinger equation(9) has to be somehow simplified whic ...
... larger molecules. The number of variables there (x,y and z coordinates for each electron and nucleus) is equal to 3*(n+N). This gives even for rather small benzene (C6H6) with 12 nuclei and 42 electrons quite large dimension of 162. Thus, the Schrödinger equation(9) has to be somehow simplified whic ...
The Chiral Constituent Quark Model (cCQM)
... ✰ To obtain LL and NL interaction potentials by using a constituent quark model whose parameters are already fixed from other sectors, so that it is fully predictive. ✰ To study what can we infer from this model about the H dibaryon. ...
... ✰ To obtain LL and NL interaction potentials by using a constituent quark model whose parameters are already fixed from other sectors, so that it is fully predictive. ✰ To study what can we infer from this model about the H dibaryon. ...
- Philsci
... gravitational and electrostatic self-interactions of its wave function. This not only violates the superposition principle of quantum mechanics but also contradicts experimental observations. Thus the wave function cannot be a description of a physical field but a description of the ergodic motion o ...
... gravitational and electrostatic self-interactions of its wave function. This not only violates the superposition principle of quantum mechanics but also contradicts experimental observations. Thus the wave function cannot be a description of a physical field but a description of the ergodic motion o ...
Claude Cohen-Tannoudji Scott Lectures Cambridge, March 9 2011
... Can we calculate the phase shift between the 2 wave functions due to various causes (free propagation, laser, external or inertial fields)? The 2 possible paths are represented in the figure above by lines which suggest trajectories of the particles. These trajectories have no meaning in quantum mec ...
... Can we calculate the phase shift between the 2 wave functions due to various causes (free propagation, laser, external or inertial fields)? The 2 possible paths are represented in the figure above by lines which suggest trajectories of the particles. These trajectories have no meaning in quantum mec ...
4.2 Notes - Seymour ISD
... The Heisenberg Uncertainty Principle • German physicist Werner Heisenberg proposed that any attempt to locate a specific electron with a photon knocks the electron off its course. • The Heisenberg uncertainty principle states that it is impossible to determine simultaneously both the position and ve ...
... The Heisenberg Uncertainty Principle • German physicist Werner Heisenberg proposed that any attempt to locate a specific electron with a photon knocks the electron off its course. • The Heisenberg uncertainty principle states that it is impossible to determine simultaneously both the position and ve ...
presentation
... The transition rate can be used to tune the system. For an arbitrary 2-component system the decoupling on the level of the wave equation (physical acoustics) puts strong tuning parameter onto the system. The dispersion relation obtained from the two Klein-Gordon equations is Lorentz invariant, the ...
... The transition rate can be used to tune the system. For an arbitrary 2-component system the decoupling on the level of the wave equation (physical acoustics) puts strong tuning parameter onto the system. The dispersion relation obtained from the two Klein-Gordon equations is Lorentz invariant, the ...
Quantum Mechanics of Many-Electrons Systems and the Theories of
... particles’ states; c) to interpret the formation of chemical bonds in terms of individual 1electron states from the isolated atoms. Another important requirement is that an IPM should provide approximate wave functions presenting all the essential symmetries of the exact ones. This is the only guara ...
... particles’ states; c) to interpret the formation of chemical bonds in terms of individual 1electron states from the isolated atoms. Another important requirement is that an IPM should provide approximate wave functions presenting all the essential symmetries of the exact ones. This is the only guara ...
Path Integrals in Quantum Mechanics
... slit experiment. Quantum mechanical particles, e.g. electrons, give rise to an interference pattern, just like waves, when they are allowed to pass through a pair of slits. The interference phenomenon occurs even when they are shot through the slits one particle at a time. This strange behavior is d ...
... slit experiment. Quantum mechanical particles, e.g. electrons, give rise to an interference pattern, just like waves, when they are allowed to pass through a pair of slits. The interference phenomenon occurs even when they are shot through the slits one particle at a time. This strange behavior is d ...
Theoretical Physics T2 Quantum Mechanics
... the foundation of quantum mechanics. A metal surface emits electrons when illuminated by ultraviolet light. The importance of this discovery lies within the inability of classical physics to describe the effect in its full extent based on three observations. 1. ) The kinetic energy of the emitted el ...
... the foundation of quantum mechanics. A metal surface emits electrons when illuminated by ultraviolet light. The importance of this discovery lies within the inability of classical physics to describe the effect in its full extent based on three observations. 1. ) The kinetic energy of the emitted el ...
Wave function

A wave function in quantum mechanics describes the quantum state of an isolated system of one or more particles. There is one wave function containing all the information about the entire system, not a separate wave function for each particle in the system. Its interpretation is that of a probability amplitude. Quantities associated with measurements, such as the average momentum of a particle, can be derived from the wave function. It is a central entity in quantum mechanics and is important in all modern theories, like quantum field theory incorporating quantum mechanics, while its interpretation may differ. The most common symbols for a wave function are the Greek letters ψ or Ψ (lower-case and capital psi).For a given system, once a representation corresponding to a maximal set of commuting observables and a suitable coordinate system is chosen, the wave function is a complex-valued function of the system's degrees of freedom corresponding to the chosen representation and coordinate system, continuous as well as discrete. Such a set of observables, by a postulate of quantum mechanics, are Hermitian linear operators on the space of states representing a set of physical observables, like position, momentum and spin that can, in principle, be simultaneously measured with arbitrary precision. Wave functions can be added together and multiplied by complex numbers to form new wave functions, and hence are elements of a vector space. This is the superposition principle of quantum mechanics. This vector space is endowed with an inner product such that it is a complete metric topological space with respect to the metric induced by the inner product. In this way the set of wave functions for a system form a function space that is a Hilbert space. The inner product is a measure of the overlap between physical states and is used in the foundational probabilistic interpretation of quantum mechanics, the Born rule, relating transition probabilities to inner products. The actual space depends on the system's degrees of freedom (hence on the chosen representation and coordinate system) and the exact form of the Hamiltonian entering the equation governing the dynamical behavior. In the non-relativistic case, disregarding spin, this is the Schrödinger equation.The Schrödinger equation determines the allowed wave functions for the system and how they evolve over time. A wave function behaves qualitatively like other waves, such as water waves or waves on a string, because the Schrödinger equation is mathematically a type of wave equation. This explains the name ""wave function"", and gives rise to wave–particle duality. The wave of the wave function, however, is not a wave in physical space; it is a wave in an abstract mathematical ""space"", and in this respect it differs fundamentally from water waves or waves on a string.For a given system, the choice of which relevant degrees of freedom to use are not unique, and correspondingly the domain of the wave function is not unique. It may be taken to be a function of all the position coordinates of the particles over position space, or the momenta of all the particles over momentum space, the two are related by a Fourier transform. These descriptions are the most important, but they are not the only possibilities. Just like in classical mechanics, canonical transformations may be used in the description of a quantum system. Some particles, like electrons and photons, have nonzero spin, and the wave function must include this fundamental property as an intrinsic discrete degree of freedom. In general, for a particle with half-integer spin the wave function is a spinor, for a particle with integer spin the wave function is a tensor. Particles with spin zero are called scalar particles, those with spin 1 vector particles, and more generally for higher integer spin, tensor particles. The terminology derives from how the wave functions transform under a rotation of the coordinate system. No elementary particle with spin 3⁄2 or higher is known, except for the hypothesized spin 2 graviton. Other discrete variables can be included, such as isospin. When a system has internal degrees of freedom, the wave function at each point in the continuous degrees of freedom (e.g. a point in space) assigns a complex number for each possible value of the discrete degrees of freedom (e.g. z-component of spin). These values are often displayed in a column matrix (e.g. a 2 × 1 column vector for a non-relativistic electron with spin 1⁄2).In the Copenhagen interpretation, an interpretation of quantum mechanics, the squared modulus of the wave function, |ψ|2, is a real number interpreted as the probability density of measuring a particle as being at a given place at a given time or having a definite momentum, and possibly having definite values for discrete degrees of freedom. The integral of this quantity, over all the system's degrees of freedom, must be 1 in accordance with the probability interpretation, this general requirement a wave function must satisfy is called the normalization condition. Since the wave function is complex valued, only its relative phase and relative magnitude can be measured. Its value does not in isolation tell anything about the magnitudes or directions of measurable observables; one has to apply quantum operators, whose eigenvalues correspond to sets of possible results of measurements, to the wave function ψ and calculate the statistical distributions for measurable quantities.The unit of measurement for ψ depends on the system, and can be found by dimensional analysis of the normalization condition for the system. For one particle in three dimensions, its units are [length]−3/2, because an integral of |ψ|2 over a region of three-dimensional space is a dimensionless probability.