
Document
... Now apply the inverse of the error transform Ei0 to the first n + k qubits to get the corrected state ...
... Now apply the inverse of the error transform Ei0 to the first n + k qubits to get the corrected state ...
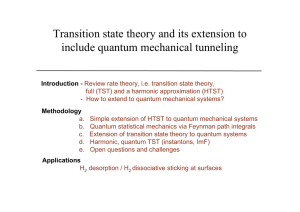
Transition state theory and its extension to include quantum
... “In view of [its] success, it is unfortunate that the theory [TST] does not enjoy a better understanding and confidence among non-specialists. Some of this difficulty can be traced to the rather unconvincing derivations of the [TST] expression for the rate constant which are found in many physical c ...
... “In view of [its] success, it is unfortunate that the theory [TST] does not enjoy a better understanding and confidence among non-specialists. Some of this difficulty can be traced to the rather unconvincing derivations of the [TST] expression for the rate constant which are found in many physical c ...
PDF
... same probability distribution – this happens when the ratios for each coordinate are complex numbers. However, it is not true that if two quantum states give the same probability distribution, then applying any unitary operator to both of them also yields quantum states giving the same probability d ...
... same probability distribution – this happens when the ratios for each coordinate are complex numbers. However, it is not true that if two quantum states give the same probability distribution, then applying any unitary operator to both of them also yields quantum states giving the same probability d ...
Quantum theory and atomic structure
... be stable and reproducible. In most cases, the source emits many wavelengths. ...
... be stable and reproducible. In most cases, the source emits many wavelengths. ...
L 33 Modern Physics [1] Modern Physics
... not explain phenomena at the atomic level • This is not too surprising since Newton’s laws were discovered by considering the behavior of macroscopic objects, like planets • Physical “laws” have a limited range of applicability, and must continually be tested to find their limitations, and then m ...
... not explain phenomena at the atomic level • This is not too surprising since Newton’s laws were discovered by considering the behavior of macroscopic objects, like planets • Physical “laws” have a limited range of applicability, and must continually be tested to find their limitations, and then m ...
Quantum Information and the Representation Theory of the
... results that establish the link between quantum information and the representation theory of the symmetric group, and to briefly mention a few of the interesting consequences that have emerged from this connection, which have to do with the Kronecker coefficients and multipartite entanglement. The p ...
... results that establish the link between quantum information and the representation theory of the symmetric group, and to briefly mention a few of the interesting consequences that have emerged from this connection, which have to do with the Kronecker coefficients and multipartite entanglement. The p ...
1. dia
... electrons is quantized so they can have only one value. The energy values are determined by the n principal quantum number. The quantum mechanics is proved that there are sublevels of the given energy levels that is why the n principal quantum number is not enough and more other quantum numbers are ...
... electrons is quantized so they can have only one value. The energy values are determined by the n principal quantum number. The quantum mechanics is proved that there are sublevels of the given energy levels that is why the n principal quantum number is not enough and more other quantum numbers are ...
L 34 Modern Physics [1]
... not explain phenomena at the atomic level • This is not too surprising since Newton’s laws were discovered by considering the behavior of macroscopic objects, like planets • Physical “laws” have a limited range of applicability, and must continually be tested to find their limitations, and then modi ...
... not explain phenomena at the atomic level • This is not too surprising since Newton’s laws were discovered by considering the behavior of macroscopic objects, like planets • Physical “laws” have a limited range of applicability, and must continually be tested to find their limitations, and then modi ...
pdf
... the later stages of both courses. The two slides shown in Figure 2 are illustrative of how the differences between the two courses could be more subtle, yet still significant. Both slides summarize the results for the system referred to in PHYS3A as the Infinite Square Well, but which Instructor B c ...
... the later stages of both courses. The two slides shown in Figure 2 are illustrative of how the differences between the two courses could be more subtle, yet still significant. Both slides summarize the results for the system referred to in PHYS3A as the Infinite Square Well, but which Instructor B c ...
Deutsch-Jozsa Paper
... so by evaluating a function. For example, a factorization program will always find the same factor of a given input. Which factor it finds could be specified by an additional constraint, narrowing the task to a function evaluation. Therefore when solving problems a classical computer cannot help per ...
... so by evaluating a function. For example, a factorization program will always find the same factor of a given input. Which factor it finds could be specified by an additional constraint, narrowing the task to a function evaluation. Therefore when solving problems a classical computer cannot help per ...
Quantum Mechanics Basics
... Consider a particle in 1D “box” (−L ≤ x ≤ L) A state of the particle is described by a continuous complex valued function ψ(x) called the “wavefunction”! Thus the set of all possible states of the particle from a vector (Hilbert) space RL ∗ The wavefunction satisfies −L ψ (x)ψ(x)dx = 1 ...
... Consider a particle in 1D “box” (−L ≤ x ≤ L) A state of the particle is described by a continuous complex valued function ψ(x) called the “wavefunction”! Thus the set of all possible states of the particle from a vector (Hilbert) space RL ∗ The wavefunction satisfies −L ψ (x)ψ(x)dx = 1 ...
REVIEW LETTERS
... have been performed and clearly favor quantum mechanics. Experiments using pairs of visible photons emitted in atomic radiative cascades seem to achieve a good realization of the ideal Gedankenexperiment. ' However, all these experiments have been performed with static setups, in which polarizers ar ...
... have been performed and clearly favor quantum mechanics. Experiments using pairs of visible photons emitted in atomic radiative cascades seem to achieve a good realization of the ideal Gedankenexperiment. ' However, all these experiments have been performed with static setups, in which polarizers ar ...
Quantum-confined Stark effect at 1.3 µm in Ge/SiGe quantum
... lifted-off for both n and p contacts. The schematic view and optical microscope image of the fabricated device are show in figure (1). III. ...
... lifted-off for both n and p contacts. The schematic view and optical microscope image of the fabricated device are show in figure (1). III. ...
Quantum key distribution
Quantum key distribution (QKD) uses quantum mechanics to guarantee secure communication. It enables two parties to produce a shared random secret key known only to them, which can then be used to encrypt and decrypt messages. It is often incorrectly called quantum cryptography, as it is the most well known example of the group of quantum cryptographic tasks.An important and unique property of quantum key distribution is the ability of the two communicating users to detect the presence of any third party trying to gain knowledge of the key. This results from a fundamental aspect of quantum mechanics: the process of measuring a quantum system in general disturbs the system. A third party trying to eavesdrop on the key must in some way measure it, thus introducing detectable anomalies. By using quantum superpositions or quantum entanglement and transmitting information in quantum states, a communication system can be implemented which detects eavesdropping. If the level of eavesdropping is below a certain threshold, a key can be produced that is guaranteed to be secure (i.e. the eavesdropper has no information about it), otherwise no secure key is possible and communication is aborted.The security of encryption that uses quantum key distribution relies on the foundations of quantum mechanics, in contrast to traditional public key cryptography which relies on the computational difficulty of certain mathematical functions, and cannot provide any indication of eavesdropping at any point in the communication process, or any mathematical proof as to the actual complexity of reversing the one-way functions used. QKD has provable security based on information theory, and forward secrecy.Quantum key distribution is only used to produce and distribute a key, not to transmit any message data. This key can then be used with any chosen encryption algorithm to encrypt (and decrypt) a message, which can then be transmitted over a standard communication channel. The algorithm most commonly associated with QKD is the one-time pad, as it is provably secure when used with a secret, random key. In real world situations, it is often also used with encryption using symmetric key algorithms like the Advanced Encryption Standard algorithm. In the case of QKD this comparison is based on the assumption of perfect single-photon sources and detectors, that cannot be easily implemented.




![L 33 Modern Physics [1] Modern Physics](http://s1.studyres.com/store/data/003217156_1-265c5a519e2bca3f33717b4abd842898-300x300.png)




![L 34 Modern Physics [1]](http://s1.studyres.com/store/data/008622077_1-047a8df5b8f51427a7d951942e25e95f-300x300.png)












