6.2.1 Geometry Review Flash Cards
... unlike stars, geometric points have no size. Think of them as being so small that they take up zero amount of space. • A point may be represented by a dot on a piece of paper. • A point is usually named with a capital letter…A ...
... unlike stars, geometric points have no size. Think of them as being so small that they take up zero amount of space. • A point may be represented by a dot on a piece of paper. • A point is usually named with a capital letter…A ...
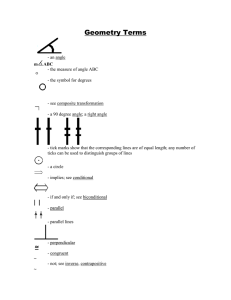
Postulates – Something you except as true
... 5. If two planes intersect, they intersect in exactly one line. 6. Segment Addition Postulate: If B is between A and C, then AB + BC = AC 7. Angle Addition Postulate: If S is in the interior of
... 5. If two planes intersect, they intersect in exactly one line. 6. Segment Addition Postulate: If B is between A and C, then AB + BC = AC 7. Angle Addition Postulate: If S is in the interior of
Improve sensor orientation using both drop-ball and
... shots to determine the location and orientation of OBS stations. Besides, Di Siena et al. (1984) proposed a power maximization approach to obtain the azimuthal orientation of three-component geophones in a vertical observation well, which consists on maximizing the signal energy of the first P-wave ...
... shots to determine the location and orientation of OBS stations. Besides, Di Siena et al. (1984) proposed a power maximization approach to obtain the azimuthal orientation of three-component geophones in a vertical observation well, which consists on maximizing the signal energy of the first P-wave ...
Unit 01-Vocab-Blank SE G2A
... another point. It has a finite length A straight path that has a beginning but no end is called a ray. A point that begins or ends a line segment or begins a ray is called an endpoint A statement we are asked to accept as true is called a postulate (or axiom). ...
... another point. It has a finite length A straight path that has a beginning but no end is called a ray. A point that begins or ends a line segment or begins a ray is called an endpoint A statement we are asked to accept as true is called a postulate (or axiom). ...
in radians - cszymanski
... What is a Radian? Before we begin our investigation of a radian let us first establish a definition of an angle and review some important concepts from geometry. Definition of an Angle: A union of two rays with a common endpoint (vertex). One side remains fixed and the other side rotates to form an ...
... What is a Radian? Before we begin our investigation of a radian let us first establish a definition of an angle and review some important concepts from geometry. Definition of an Angle: A union of two rays with a common endpoint (vertex). One side remains fixed and the other side rotates to form an ...
Notes 38
... Vocabulary Point- an exact location. It is usually represented as a dot, but it has no size at all. Line- a straight path that extends without end in opposite directions. Plane- a flat surface that has no thickness and extends forever. Ray- a part of a line. It has one endpoint and extends forever ...
... Vocabulary Point- an exact location. It is usually represented as a dot, but it has no size at all. Line- a straight path that extends without end in opposite directions. Plane- a flat surface that has no thickness and extends forever. Ray- a part of a line. It has one endpoint and extends forever ...