Venous Collateral Circulation of the Extracranial
... system (Fig. 1). The anatomical pathways of jugular drainage are well established. The main jugular blood drainage pathway leads from the SSS and the transverse sinuses via the sigmoid sinuses into the IJVs, which meet the superior cava vein via the brachiocephalic vein. Several ultrasound study of ...
... system (Fig. 1). The anatomical pathways of jugular drainage are well established. The main jugular blood drainage pathway leads from the SSS and the transverse sinuses via the sigmoid sinuses into the IJVs, which meet the superior cava vein via the brachiocephalic vein. Several ultrasound study of ...
3-Major Veins of the Body
... o Umbilical veins2. o There are two types of veins*: 1. Superficial veins: close to the surface of the body NO corresponding arteries 2. Deep veins: found deeper in the body With corresponding arteries (venae comitantes) ...
... o Umbilical veins2. o There are two types of veins*: 1. Superficial veins: close to the surface of the body NO corresponding arteries 2. Deep veins: found deeper in the body With corresponding arteries (venae comitantes) ...
No. 17 - 辽宁医学院
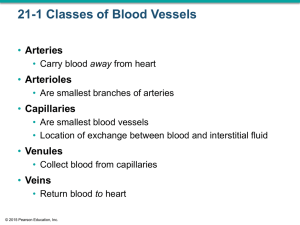
... steadily increase, whereas the total crosssectional area of parallel vessels decreases. Venous pressure is always lower than arterial pressure, and the walls of the veins are never as thick as the walls of the corresponding arteries. The veins consist of the pulmonary and systemic ones. ...
... steadily increase, whereas the total crosssectional area of parallel vessels decreases. Venous pressure is always lower than arterial pressure, and the walls of the veins are never as thick as the walls of the corresponding arteries. The veins consist of the pulmonary and systemic ones. ...
File
... steadily increase, whereas the total crosssectional area of parallel vessels decreases. Venous pressure is always lower than arterial pressure, and the walls of the veins are never as thick as the walls of the corresponding arteries. The veins consist of the pulmonary and systemic ones. ...
... steadily increase, whereas the total crosssectional area of parallel vessels decreases. Venous pressure is always lower than arterial pressure, and the walls of the veins are never as thick as the walls of the corresponding arteries. The veins consist of the pulmonary and systemic ones. ...
(updated) Heart-MBVS-veins-2016
... Veins are blood vessels that bring blood back to the heart. All veins carry deoxygenated blood with the exception of the pulmonary veins and umbilical veins. ...
... Veins are blood vessels that bring blood back to the heart. All veins carry deoxygenated blood with the exception of the pulmonary veins and umbilical veins. ...
AP #14L1 - Defiance City Schools
... tiny arterioles into tiny venules There is an exchange between blood & tissue fluid around the cells ...
... tiny arterioles into tiny venules There is an exchange between blood & tissue fluid around the cells ...
chapter 23-Vessels and Circulation
... • Contraction of muscles squeezes veins, forcing blood through • Works more efficiently when a person is active • When a person is inactive, blood may pool in lower extremities ...
... • Contraction of muscles squeezes veins, forcing blood through • Works more efficiently when a person is active • When a person is inactive, blood may pool in lower extremities ...
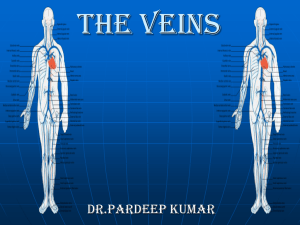
3-Major Veins of the body
... Veins are blood vessels that bring blood back to the heart. All veins carry deoxygenated blood ...
... Veins are blood vessels that bring blood back to the heart. All veins carry deoxygenated blood ...
Blood Flow
... • Automatic adjustment of blood flow to each tissue in proportion to its requirements at any given point in time • Is controlled intrinsically by modifying the diameter of local arterioles feeding the capillaries • Is independent of MAP, which is controlled as needed to maintain constant pressure ...
... • Automatic adjustment of blood flow to each tissue in proportion to its requirements at any given point in time • Is controlled intrinsically by modifying the diameter of local arterioles feeding the capillaries • Is independent of MAP, which is controlled as needed to maintain constant pressure ...
failure, and stroke
... • Automatic adjustment of blood flow to each tissue in proportion to its requirements at any given point in time • Is controlled intrinsically by modifying the diameter of local arterioles feeding the capillaries • Is independent of MAP, which is controlled as needed to maintain constant pressure ...
... • Automatic adjustment of blood flow to each tissue in proportion to its requirements at any given point in time • Is controlled intrinsically by modifying the diameter of local arterioles feeding the capillaries • Is independent of MAP, which is controlled as needed to maintain constant pressure ...
The deep veins
... The venous drainage of the lower limb can be divided into two separate systems, the deep veins and the superficial veins. These are connected by the communicating veins. The deep veins in the calf follow the same distribution as the main arteries but are usually double, forming the anterior tibial, ...
... The venous drainage of the lower limb can be divided into two separate systems, the deep veins and the superficial veins. These are connected by the communicating veins. The deep veins in the calf follow the same distribution as the main arteries but are usually double, forming the anterior tibial, ...
Extra-peritoneal Packing of Hemorrhagic Pelvic Fracture
... inferior gluteal) visceral branches (umbilical, middle vesical, inferior vesical, middle hemorrhoidal, uterine, and vaginal). Superior vesical artery arises from the umbilical artery. 4. Internal pudendal: Supplies branches to rectum, gentialia, + perineum. 5. Veins: Few valves allowing bidirectiona ...
... inferior gluteal) visceral branches (umbilical, middle vesical, inferior vesical, middle hemorrhoidal, uterine, and vaginal). Superior vesical artery arises from the umbilical artery. 4. Internal pudendal: Supplies branches to rectum, gentialia, + perineum. 5. Veins: Few valves allowing bidirectiona ...
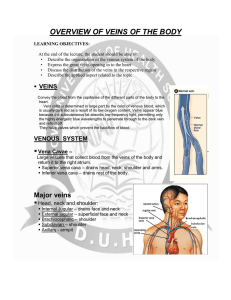
OVERVIEW OF VEINS OF THE BODY
... Convey the blood from the capillaries of the different parts of the body to the heart. Vein color is determined in large part by the color of venous blood, which is usually dark red as a result of its low oxygen content. Veins appear blue because the subcutaneous fat absorbs low frequency light, per ...
... Convey the blood from the capillaries of the different parts of the body to the heart. Vein color is determined in large part by the color of venous blood, which is usually dark red as a result of its low oxygen content. Veins appear blue because the subcutaneous fat absorbs low frequency light, per ...
Transcripts/4_6 1-2 (Zehren) without extra notes
... vessel has an extremely thin wall like a capillary where it can get its own oxygen and nutrients directly from the blood, vessels need their own blood supply and that is called the vasa vasorum (this is an important term that means vessels of the vessel) b. The thickness of the tunica media is the e ...
... vessel has an extremely thin wall like a capillary where it can get its own oxygen and nutrients directly from the blood, vessels need their own blood supply and that is called the vasa vasorum (this is an important term that means vessels of the vessel) b. The thickness of the tunica media is the e ...
NSC 201 - National Open University of Nigeria
... were the seat of certain strong emotions. A very determined person may be described as having ―a lot of heart,‖ and a person who has been disappointed romantically can be described as having a ...
... were the seat of certain strong emotions. A very determined person may be described as having ―a lot of heart,‖ and a person who has been disappointed romantically can be described as having a ...
Arteries and Veins Worksheet
... 4) The hepatic portal vein drains the digestive tract organs and carries this blood through the liver before it enters the systemic circulation. The hepatic veins drain the liver. 5) The internal iliac vein drains blood from the rectum and tissue of the bladder. 6) The common iliac vein which is for ...
... 4) The hepatic portal vein drains the digestive tract organs and carries this blood through the liver before it enters the systemic circulation. The hepatic veins drain the liver. 5) The internal iliac vein drains blood from the rectum and tissue of the bladder. 6) The common iliac vein which is for ...
Veins 1 Head and Thoracic Veins
... 3. intercostal vein 3. inferior vena cava 5. superior vena cava Select and arrange the veins in the order blood passes through them going from the esophagus to the heart. ...
... 3. intercostal vein 3. inferior vena cava 5. superior vena cava Select and arrange the veins in the order blood passes through them going from the esophagus to the heart. ...
Arteries
... – Common at joints, in abdominal organs, brain, and heart; none in retina, kidneys, spleen ...
... – Common at joints, in abdominal organs, brain, and heart; none in retina, kidneys, spleen ...
The Cardiovascular System: Blood Vessels
... closely together, forming a slick surface that minimizes friction as blood moves through the lumen. In vessels larger than 1 mm in diameter, a subendothelial layer, consisting of a basement membrane and loose connective tissue, supports the endothelium. The middle tunic, the tunica media (me⬘de-ah), ...
... closely together, forming a slick surface that minimizes friction as blood moves through the lumen. In vessels larger than 1 mm in diameter, a subendothelial layer, consisting of a basement membrane and loose connective tissue, supports the endothelium. The middle tunic, the tunica media (me⬘de-ah), ...
Transcripts/4_6 1
... 2. The structural difference between arteries and veins is primarily the degree of development of the tunica media. For any given size, the tunica media in an artery is thicker than in a vein. (The more rigid wall of an artery compared to the thinner, more collapsed wall of a vein usually makes it e ...
... 2. The structural difference between arteries and veins is primarily the degree of development of the tunica media. For any given size, the tunica media in an artery is thicker than in a vein. (The more rigid wall of an artery compared to the thinner, more collapsed wall of a vein usually makes it e ...
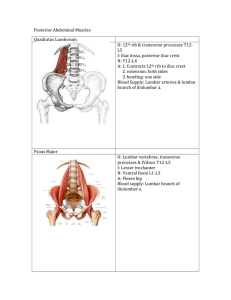
Posterior Abdominal Muscles Quadratus Lumborum O: 12th rib
... Lateral 3: Superficial branch of Lateral Plantar N. (S2, S3) A: 1. Flex MTP Blood supply: medial and lateral plantar a. ...
... Lateral 3: Superficial branch of Lateral Plantar N. (S2, S3) A: 1. Flex MTP Blood supply: medial and lateral plantar a. ...
21-7 The Systemic Circuit
... and reduce the force of heart contraction, also blocks kidneys from producing a angiotensin II, reducing the amount of angiotensin so blood vessels relax and widen, making it easier for blood to flow through; eventually a vasodilator was included to reduce the blood pressure to <140/90. ...
... and reduce the force of heart contraction, also blocks kidneys from producing a angiotensin II, reducing the amount of angiotensin so blood vessels relax and widen, making it easier for blood to flow through; eventually a vasodilator was included to reduce the blood pressure to <140/90. ...
vascular-technology-lecture-22-venous-gross
... Hepato-petal flow is blood flow into the liver Hepato-fugal flow is blood flow away from the liver Veins with valves Where the most of the valves are: the further away from the heart!! The closer to the heart, the least likely for a vein to have a valve. ...
... Hepato-petal flow is blood flow into the liver Hepato-fugal flow is blood flow away from the liver Veins with valves Where the most of the valves are: the further away from the heart!! The closer to the heart, the least likely for a vein to have a valve. ...
The Circulatory System: Blood Vessels and Circulation
... 750 Part Four Regulation and Maintenance but of course there is a smooth gradation from one category to the next: ...
... 750 Part Four Regulation and Maintenance but of course there is a smooth gradation from one category to the next: ...
Circulation - Berkeley County Schools
... • Formation of new blood vessels • Vascular endothelial growth factor (VEGF) • Occurs in the embryo as tissues and organs develop • Occurs in response to factors released by cells that are hypoxic, or oxygen-starved • Most important in cardiac muscle, where it takes place in response to a chronicall ...
... • Formation of new blood vessels • Vascular endothelial growth factor (VEGF) • Occurs in the embryo as tissues and organs develop • Occurs in response to factors released by cells that are hypoxic, or oxygen-starved • Most important in cardiac muscle, where it takes place in response to a chronicall ...
Blood

Blood is a bodily fluid in humans and other animals that delivers necessary substances such as nutrients and oxygen to the cells and transports metabolic waste products away from those same cells. When it reaches the lungs, gas exchange occurs when carbon dioxide is diffused out of the blood into the pulmonary alveoli and oxygen is diffused into the blood. This oxygenated blood is pumped to the left hand side of the heart in the pulmonary vein and enters the left atrium. From here it passes through the mitral valve, through the ventricle and taken all around the body by the aorta. Blood contains antibodies, nutrients, oxygen and much more to help the body work.In vertebrates, it is composed of blood cells suspended in blood plasma. Plasma, which constitutes 55% of blood fluid, is mostly water (92% by volume), and contains dissipated proteins, glucose, mineral ions, hormones, carbon dioxide (plasma being the main medium for excretory product transportation), and blood cells themselves. Albumin is the main protein in plasma, and it functions to regulate the colloidal osmotic pressure of blood. The blood cells are mainly red blood cells (also called RBCs or erythrocytes), white blood cells (also called WBCs or leukocytes) and platelets. The most abundant cells in vertebrate blood are red blood cells. These contain hemoglobin, an iron-containing protein, which facilitates oxygen transport by reversibly binding to this respiratory gas and greatly increasing its solubility in blood. In contrast, carbon dioxide is almost entirely transported extracellularly dissolved in plasma as bicarbonate ion.Vertebrate blood is bright red when its haemoglobin is oxygenated and dark red when it is deoxygenated. Some animals, such as crustaceans and mollusks, use hemocyanin to carry oxygen, instead of hemoglobin. Insects and some mollusks use a fluid called hemolymph instead of blood, the difference being that hemolymph is not contained in a closed circulatory system. In most insects, this ""blood"" does not contain oxygen-carrying molecules such as hemoglobin because their bodies are small enough for their tracheal system to suffice for supplying oxygen.Jawed vertebrates have an adaptive immune system, based largely on white blood cells. White blood cells help to resist infections and parasites. Platelets are important in the clotting of blood. Arthropods, using hemolymph, have hemocytes as part of their immune system.Blood is circulated around the body through blood vessels by the pumping action of the heart. In animals with lungs, arterial blood carries oxygen from inhaled air to the tissues of the body, and venous blood carries carbon dioxide, a waste product of metabolism produced by cells, from the tissues to the lungs to be exhaled.Medical terms related to blood often begin with hemo- or hemato- (also spelled haemo- and haemato-) from the Greek word αἷμα (haima) for ""blood"". In terms of anatomy and histology, blood is considered a specialized form of connective tissue, given its origin in the bones and the presence of potential molecular fibers in the form of fibrinogen.