Effect of Aluminum mole fraction and well width on the - OAM-RC
... intensity, luminescence power and the electrical characteristics. It was observed that electron probability density depends on the quantum well thickness and effective mass of the carriers of Gallium Nitride and Aluminum Gallium Nitride. The variation in the spreading of electron in the quantum well ...
... intensity, luminescence power and the electrical characteristics. It was observed that electron probability density depends on the quantum well thickness and effective mass of the carriers of Gallium Nitride and Aluminum Gallium Nitride. The variation in the spreading of electron in the quantum well ...
Section 6.2 ~ Basics of Probability
... Ex. ~ The probability of a wrong answer on a multiple choice question with five possible answers ...
... Ex. ~ The probability of a wrong answer on a multiple choice question with five possible answers ...
PROBABILITIES FOR SINGLE EVENTS
... relative frequency. In a given experiment how large does N have to be before the prediction is counted as definite? It must be large enough so the probability of error is sufficiently small to isolate a result of significance given the status of competing theories, competing groups, the consequences ...
... relative frequency. In a given experiment how large does N have to be before the prediction is counted as definite? It must be large enough so the probability of error is sufficiently small to isolate a result of significance given the status of competing theories, competing groups, the consequences ...
Hwk Set #14 - Publisher`s solutions
... The red-orange colors in the neon emission spectrum are due to transitions from excited 3p states to the lower energy but still excited 3s states. This occurs because the ground states are collisionally excited by the electrical discharge. The absorption spectrum of a gas consists of only those spec ...
... The red-orange colors in the neon emission spectrum are due to transitions from excited 3p states to the lower energy but still excited 3s states. This occurs because the ground states are collisionally excited by the electrical discharge. The absorption spectrum of a gas consists of only those spec ...
Quantum Sleeping Beauty
... not parallel. This leaves us with two options—applying the treatment of pre-branching probability from the Sleeping Beauty case to the many-worlds case, and applying the manyworlds treatment to the Sleeping Beauty case. According to the first option, the treatment of probability in the Sleeping Bea ...
... not parallel. This leaves us with two options—applying the treatment of pre-branching probability from the Sleeping Beauty case to the many-worlds case, and applying the manyworlds treatment to the Sleeping Beauty case. According to the first option, the treatment of probability in the Sleeping Bea ...
ch11.5-13
... P( Bk | A) is often called the posterior probability of Bk . 1. The Belgian 20-framk coin (B20), the Italian 500-lire coin (I500), and the Honk Kong 5-dollar (HK5) are approximately the same size. Coin purse one (C1) contains six of each of these coins. Coin purse two (C2) contains nine B20s, six I5 ...
... P( Bk | A) is often called the posterior probability of Bk . 1. The Belgian 20-framk coin (B20), the Italian 500-lire coin (I500), and the Honk Kong 5-dollar (HK5) are approximately the same size. Coin purse one (C1) contains six of each of these coins. Coin purse two (C2) contains nine B20s, six I5 ...
Planck`s quantum theory
... What happens to the particle when it is over the finite well? Imagine a particle of zero kinetic energy incident from the left. What can we say? Imagine a particle with an energy E < V0 that is in the well. What can we say? ...
... What happens to the particle when it is over the finite well? Imagine a particle of zero kinetic energy incident from the left. What can we say? Imagine a particle with an energy E < V0 that is in the well. What can we say? ...
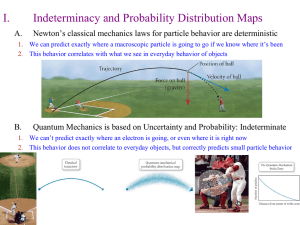
Chapter 7 Lect. 2
... 1. We can predict exactly where a macroscopic particle is going to go if we know where it’s been 2. This behavior correlates with what we see in everyday behavior of objects ...
... 1. We can predict exactly where a macroscopic particle is going to go if we know where it’s been 2. This behavior correlates with what we see in everyday behavior of objects ...
Study Guide Chap. 11
... radiation energy density vs. wavelength or frequency over temperature at different temperatures using Planck’s equation. How does it change if Wien equation or Rayleigh-Jeans equation is used? What is ultra- violet catastrophe? How do you convert wavelength to frequency? ...
... radiation energy density vs. wavelength or frequency over temperature at different temperatures using Planck’s equation. How does it change if Wien equation or Rayleigh-Jeans equation is used? What is ultra- violet catastrophe? How do you convert wavelength to frequency? ...
Diffusion quantum Monte Carlo
... of the Diffusion Equation • If we have only the first term -½2f, it is a pure random walk. • If we have first and second term, it describes a diffusion with drift ...
... of the Diffusion Equation • If we have only the first term -½2f, it is a pure random walk. • If we have first and second term, it describes a diffusion with drift ...
Presentation453.22
... There are however several differences between classical and quantum mechanics ...
... There are however several differences between classical and quantum mechanics ...
As we know, the measurement of a static (specific
... theory in lectures, conferences, and in his correspondence, arguing with Bohr in a series of thought experiments that have become part of the lore of 20th century physics.2 The fact is that quantum mechanics is puzzling for several reasons. For starts, not only are its results often very disconcerti ...
... theory in lectures, conferences, and in his correspondence, arguing with Bohr in a series of thought experiments that have become part of the lore of 20th century physics.2 The fact is that quantum mechanics is puzzling for several reasons. For starts, not only are its results often very disconcerti ...
Diffusion Quantum Monte Carlo
... • how would we solve the time-dependent equation? • Naïve approach would be to produce a grid in the x-t plane • tn=t0+n t ; xs=x0+s x ; (x,t) => (xs,tn) ...
... • how would we solve the time-dependent equation? • Naïve approach would be to produce a grid in the x-t plane • tn=t0+n t ; xs=x0+s x ; (x,t) => (xs,tn) ...
Another version - Scott Aaronson
... (2) a classical computer probably couldn’t even verify the results! Theoretical Challenge: Argue that, even with photon losses and messier initial states, you’re still solving a classically-intractable sampling problem ...
... (2) a classical computer probably couldn’t even verify the results! Theoretical Challenge: Argue that, even with photon losses and messier initial states, you’re still solving a classically-intractable sampling problem ...
Math Review - Cobb Learning
... From the graph you can see that the high on Feb 5 was 25 degrees and the low was 10 degrees. You can also see the difference between high and low temps that day was 15. ...
... From the graph you can see that the high on Feb 5 was 25 degrees and the low was 10 degrees. You can also see the difference between high and low temps that day was 15. ...
Probability amplitude

In quantum mechanics, a probability amplitude is a complex number used in describing the behaviour of systems. The modulus squared of this quantity represents a probability or probability density.Probability amplitudes provide a relationship between the wave function (or, more generally, of a quantum state vector) of a system and the results of observations of that system, a link first proposed by Max Born. Interpretation of values of a wave function as the probability amplitude is a pillar of the Copenhagen interpretation of quantum mechanics. In fact, the properties of the space of wave functions were being used to make physical predictions (such as emissions from atoms being at certain discrete energies) before any physical interpretation of a particular function was offered. Born was awarded half of the 1954 Nobel Prize in Physics for this understanding (see #References), and the probability thus calculated is sometimes called the ""Born probability"". These probabilistic concepts, namely the probability density and quantum measurements, were vigorously contested at the time by the original physicists working on the theory, such as Schrödinger and Einstein. It is the source of the mysterious consequences and philosophical difficulties in the interpretations of quantum mechanics—topics that continue to be debated even today.