Summary of Objectives
... patterns for special right triangles. Study guide – Case 1 & Case 2 (Begin Wednesday’s notes) ...
... patterns for special right triangles. Study guide – Case 1 & Case 2 (Begin Wednesday’s notes) ...
On the works of Euler and his followers on spherical geometry
... In all the discussion that follows, the distance on the sphere is the angular distance. In other words, we take the model of the unit sphere in 3-space, where the distance between two points is equal to the angle made by the two rays starting at the origin and passing through these points. A spheric ...
... In all the discussion that follows, the distance on the sphere is the angular distance. In other words, we take the model of the unit sphere in 3-space, where the distance between two points is equal to the angle made by the two rays starting at the origin and passing through these points. A spheric ...
ISOSPECTRAL AND ISOSCATTERING MANIFOLDS: A SURVEY
... is a cutoff function, the ϕj are resonance eigenfunctions, and the numbers cj,k depend on the initial data ψ. The secular terms (involving powers of t) may arise because the resonances are solutions of a non-self-adjoint eigenvalue problem. More precisely, the resonances are poles of the analyticall ...
... is a cutoff function, the ϕj are resonance eigenfunctions, and the numbers cj,k depend on the initial data ψ. The secular terms (involving powers of t) may arise because the resonances are solutions of a non-self-adjoint eigenvalue problem. More precisely, the resonances are poles of the analyticall ...
On Klein`s So-called Non
... and is therefore more difficult to visualize than the Euclidean. One more difficulty is due to the fact that several among the founders of the subject had their particular point of view, and they had different opinions of what the fundamental notions should be. ...
... and is therefore more difficult to visualize than the Euclidean. One more difficulty is due to the fact that several among the founders of the subject had their particular point of view, and they had different opinions of what the fundamental notions should be. ...
Tangent circles in the hyperbolic disk - Rose
... statements that are universally accepted as true without requiring a proof. Hyperbolic geometry follows the first four of these axioms, but not the fifth axiom, the Parallel Postulate. One negation of the Parallel Postulate says, “Through a point not on a line, there are many lines parallel to the g ...
... statements that are universally accepted as true without requiring a proof. Hyperbolic geometry follows the first four of these axioms, but not the fifth axiom, the Parallel Postulate. One negation of the Parallel Postulate says, “Through a point not on a line, there are many lines parallel to the g ...
THE GEOMETRIES OF 3
... the theory in addition to the use of purely topological methods. The basic aim of this article is to discuss the various geometries which arise and explain their significance for the theory of 3-manifolds. The idea is that many 3-manifolds admit 'nice' metrics which give one new insight into propert ...
... the theory in addition to the use of purely topological methods. The basic aim of this article is to discuss the various geometries which arise and explain their significance for the theory of 3-manifolds. The idea is that many 3-manifolds admit 'nice' metrics which give one new insight into propert ...
kucukarslan et al.
... membership function which assigns to each object a grade of membership ranging between zero and one. One of the main goals in the fuzzy sets theory is to give fuzzification of different classical mathematical structures and to study properties of these fuzzy objects. Many scientists have studied fuz ...
... membership function which assigns to each object a grade of membership ranging between zero and one. One of the main goals in the fuzzy sets theory is to give fuzzification of different classical mathematical structures and to study properties of these fuzzy objects. Many scientists have studied fuz ...
Pants decompositions of random surfaces
... Our lower bound is a lot stronger than the one coming from the Buser-Sarnak estimate. Instead of improving the trivial bound by a factor of log g, we improve it by a polynomial factor g 1/6−ε . Let’s take a moment to explain why it is difficult to prove such a lower bound. Almost all the random hype ...
... Our lower bound is a lot stronger than the one coming from the Buser-Sarnak estimate. Instead of improving the trivial bound by a factor of log g, we improve it by a polynomial factor g 1/6−ε . Let’s take a moment to explain why it is difficult to prove such a lower bound. Almost all the random hype ...
On characterizations of Euclidean spaces
... Nico Düvelmeyer. Angle measures and bisectors in Minkowski planes. Canadian Mathematical Bulletin, to appear. Nico Düvelmeyer. On convex bodies all whose two-dimensional sections are equiframed. to be submitted ...
... Nico Düvelmeyer. Angle measures and bisectors in Minkowski planes. Canadian Mathematical Bulletin, to appear. Nico Düvelmeyer. On convex bodies all whose two-dimensional sections are equiframed. to be submitted ...
What is Hyperbolic Geometry? - School of Mathematics, TIFR
... Gauss started thinking of parallels about 1792. In an 18th November, 1824 letter to F. A. Taurinus, he wrote: ‘The assumption that the sum of the three angles (of a triangle) is smaller than two right angles leads to a geometry which is quite different from our (Euclidean) geometry, but which is in ...
... Gauss started thinking of parallels about 1792. In an 18th November, 1824 letter to F. A. Taurinus, he wrote: ‘The assumption that the sum of the three angles (of a triangle) is smaller than two right angles leads to a geometry which is quite different from our (Euclidean) geometry, but which is in ...
What is Hyperbolic Geometry?
... Gauss started thinking of parallels about 1792. In an 18th November, 1824 letter to F. A. Taurinus, he wrote: ‘The assumption that the sum of the three angles (of a triangle) is smaller than two right angles leads to a geometry which is quite different from our (Euclidean) geometry, but which is in ...
... Gauss started thinking of parallels about 1792. In an 18th November, 1824 letter to F. A. Taurinus, he wrote: ‘The assumption that the sum of the three angles (of a triangle) is smaller than two right angles leads to a geometry which is quite different from our (Euclidean) geometry, but which is in ...
optimal angle bounds for quadrilateral meshes
... construct an explicit mesh in each of them. The thick parts are more complicated, but we can use a conformal map to transfer a mesh from the unit disk, D, to the thick parts of Ω with small distortion. The mesh on D is produced using a finite piece of an infinite tesselation of D by hyperbolic penta ...
... construct an explicit mesh in each of them. The thick parts are more complicated, but we can use a conformal map to transfer a mesh from the unit disk, D, to the thick parts of Ω with small distortion. The mesh on D is produced using a finite piece of an infinite tesselation of D by hyperbolic penta ...
On Lobachevsky`s trigonometric formulae
... these formulae use the embedding of the sphere in the ambient three-space, where the sides of triangles are arcs of great circles, that is, intersections of the sphere with planes passing through the origin, and the angles of triangles are the dihedral angles between the corresponding Euclidean plan ...
... these formulae use the embedding of the sphere in the ambient three-space, where the sides of triangles are arcs of great circles, that is, intersections of the sphere with planes passing through the origin, and the angles of triangles are the dihedral angles between the corresponding Euclidean plan ...
On Lobachevsky`s trigonometric formulae
... these formulae use the embedding of the sphere in the ambient three-space, where the sides of triangles are arcs of great circles, that is, intersections of the sphere with planes passing through the origin, and the angles of triangles are the dihedral angles between the corresponding Euclidean plan ...
... these formulae use the embedding of the sphere in the ambient three-space, where the sides of triangles are arcs of great circles, that is, intersections of the sphere with planes passing through the origin, and the angles of triangles are the dihedral angles between the corresponding Euclidean plan ...
Curriculum Map
... C: Parallel and Perpendicular Lines C1: Properties of Parallel Lines C2: Proving lines parallel C3: Parallel and perpendicular lines C4: Parallel lines and triangle-sum theorem C5: The Polygon Angle-Sum Theorem C6: Lines in the Coordinate Plane C7: Slopes of Parallel and Perpendicular Lines ...
... C: Parallel and Perpendicular Lines C1: Properties of Parallel Lines C2: Proving lines parallel C3: Parallel and perpendicular lines C4: Parallel lines and triangle-sum theorem C5: The Polygon Angle-Sum Theorem C6: Lines in the Coordinate Plane C7: Slopes of Parallel and Perpendicular Lines ...
Katie Hoppe - STMA Schools
... area of a prism and cylinder. LT 4 I can find the volume of a prism and cylinder. LT 5 I can find the surface area of a pyramid and cone. LT 6 I can find the volume of a pyramid and cone. LT 7 I can find the surface area of a sphere. LT 8 I can find the volume of a sphere. LT 9 I can use relationshi ...
... area of a prism and cylinder. LT 4 I can find the volume of a prism and cylinder. LT 5 I can find the surface area of a pyramid and cone. LT 6 I can find the volume of a pyramid and cone. LT 7 I can find the surface area of a sphere. LT 8 I can find the volume of a sphere. LT 9 I can use relationshi ...
Chapter 3
... Geometry introduced in Section 3.1 along with several very important examples based on the notion of projective geometries, which first arose in Renaissance art in attempts to represent three-dimensional scenes on a two-dimensional canvas. Both Euclidean and hyperbolic geometry can be realized in th ...
... Geometry introduced in Section 3.1 along with several very important examples based on the notion of projective geometries, which first arose in Renaissance art in attempts to represent three-dimensional scenes on a two-dimensional canvas. Both Euclidean and hyperbolic geometry can be realized in th ...
Chapter 16 - BISD Moodle
... •30. Both curves cannot correspond to lines. (Lines are great circles and great circles divide the sphere into two equal hemispheres. If one of these curves divides the sphere into two equal hemispheres, the other one clearly does not.) Euclidean and Sphere Geometries. •31. One. •32. No. 33. That th ...
... •30. Both curves cannot correspond to lines. (Lines are great circles and great circles divide the sphere into two equal hemispheres. If one of these curves divides the sphere into two equal hemispheres, the other one clearly does not.) Euclidean and Sphere Geometries. •31. One. •32. No. 33. That th ...
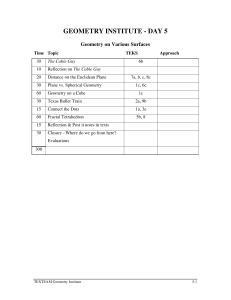
geometry institute - day 5
... This problem is a variation of the Spider and the Fly problem. After solving the problem, most people will realize that building a model and/or drawing a net is an effective problem solving tool. Reducing the rooms to their plane nets makes the problem much simpler. The problem leads to the definiti ...
... This problem is a variation of the Spider and the Fly problem. After solving the problem, most people will realize that building a model and/or drawing a net is an effective problem solving tool. Reducing the rooms to their plane nets makes the problem much simpler. The problem leads to the definiti ...
MA352_Differential_Geometry_CIIT_VU
... The next name we came across in the history of geometry is Archimedes. He understood the geometry of different objects about him, for example, he calculated the area and volumes of different objects, and the techniques were later formulated in calculus. He understood geometry to such an extent that ...
... The next name we came across in the history of geometry is Archimedes. He understood the geometry of different objects about him, for example, he calculated the area and volumes of different objects, and the techniques were later formulated in calculus. He understood geometry to such an extent that ...
Pdf slides - Daniel Mathews
... the right of the door a little knot had formed round a small table, the center of which was the mathematics student, who was eagerly talking. He had made the assertion that one could draw through a given point more than one parallel to a straight line; Frau Hagenström had cried out that this was imp ...
... the right of the door a little knot had formed round a small table, the center of which was the mathematics student, who was eagerly talking. He had made the assertion that one could draw through a given point more than one parallel to a straight line; Frau Hagenström had cried out that this was imp ...
Non Euclidean Geometry
... Euclid (ca 300 BC) The first to write down the postulates for what is now known as Euclidean geometry. He was associated with the famous School of Alexandria. Archimedes (ca 225 BC) Pliny called him “the God of Mathematics”. He was also associated with the School of Alexandria. His name is now assoc ...
... Euclid (ca 300 BC) The first to write down the postulates for what is now known as Euclidean geometry. He was associated with the famous School of Alexandria. Archimedes (ca 225 BC) Pliny called him “the God of Mathematics”. He was also associated with the School of Alexandria. His name is now assoc ...
Slides for Nov. 12, 2014, lecture
... on one’s method of presentation), these relations also include other quantitative relations among geometrical objects living in the manifold, such as the angle between two intersecting curves (conformal structure), the volume of a solid figure (volume element), the intrinsic curvature of a curve, et ...
... on one’s method of presentation), these relations also include other quantitative relations among geometrical objects living in the manifold, such as the angle between two intersecting curves (conformal structure), the volume of a solid figure (volume element), the intrinsic curvature of a curve, et ...
LYAPUNOV EXPONENTS IN HILBERT GEOMETRY
... It then asks the question of knowing if weak regularity would not imply regularity. In other words, is the last property satisfied for all approximately regular functions ? 1.3. Contents. The geodesic flow of Hilbert metrics has been studied by Yves Benoist in [Ben04] and by myself in [Cra09]. In th ...
... It then asks the question of knowing if weak regularity would not imply regularity. In other words, is the last property satisfied for all approximately regular functions ? 1.3. Contents. The geodesic flow of Hilbert metrics has been studied by Yves Benoist in [Ben04] and by myself in [Cra09]. In th ...
Hyperbolic Geometry - DigitalCommons@University of Nebraska
... not on a given straight line, one and only one line can be drawn that never meets the given line.), mathematicians were still troubled by it’s complexity, and were convinced that it could be proven as a theorem using the other four axioms. Many tried to find a proof by contradiction. They either ass ...
... not on a given straight line, one and only one line can be drawn that never meets the given line.), mathematicians were still troubled by it’s complexity, and were convinced that it could be proven as a theorem using the other four axioms. Many tried to find a proof by contradiction. They either ass ...
Differential geometry of surfaces

In mathematics, the differential geometry of surfaces deals with smooth surfaces with various additional structures, most often, a Riemannian metric.Surfaces have been extensively studied from various perspectives: extrinsically, relating to their embedding in Euclidean space and intrinsically, reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. One of the fundamental concepts investigated is the Gaussian curvature, first studied in depth by Carl Friedrich Gauss (articles of 1825 and 1827), who showed that curvature was an intrinsic property of a surface, independent of its isometric embedding in Euclidean space.Surfaces naturally arise as graphs of functions of a pair of variables, and sometimes appear in parametric form or as loci associated to space curves. An important role in their study has been played by Lie groups (in the spirit of the Erlangen program), namely the symmetry groups of the Euclidean plane, the sphere and the hyperbolic plane. These Lie groups can be used to describe surfaces of constant Gaussian curvature; they also provide an essential ingredient in the modern approach to intrinsic differential geometry through connections. On the other hand extrinsic properties relying on an embedding of a surface in Euclidean space have also been extensively studied. This is well illustrated by the non-linear Euler–Lagrange equations in the calculus of variations: although Euler developed the one variable equations to understand geodesics, defined independently of an embedding, one of Lagrange's main applications of the two variable equations was to minimal surfaces, a concept that can only be defined in terms of an embedding.