On Linear Inference
... what do we mean? To discuss this, some terminology: we say “even(t)” is a proposition and “even(t) true” is a judgment. Following Martin-Löf, a judgment is an object of knowledge. We obtain knowledge by making inferences from judgments we already know. We can then read the rule above as If we know ...
... what do we mean? To discuss this, some terminology: we say “even(t)” is a proposition and “even(t) true” is a judgment. Following Martin-Löf, a judgment is an object of knowledge. We obtain knowledge by making inferences from judgments we already know. We can then read the rule above as If we know ...
Tactical and Strategic Challenges to Logic (KAIST
... and bolts. As we have it now, inconsistency-robustness has a large but still quite selective providence. In recent writings, I have suggested that it is a property that travels well, rather in the way that Swiss wine is believed not to.8 What I mean by this is that it is a property that appears to b ...
... and bolts. As we have it now, inconsistency-robustness has a large but still quite selective providence. In recent writings, I have suggested that it is a property that travels well, rather in the way that Swiss wine is believed not to.8 What I mean by this is that it is a property that appears to b ...
Propositional Logic
... – Standard technique is to index facts with the time when they’re true – This means we have a separate KB for every time point ...
... – Standard technique is to index facts with the time when they’re true – This means we have a separate KB for every time point ...
Section.8.3
... The order of a predicate is 1 if its arguments are terms. Otherwise the order is n + 1 where n is the maximum order of the arguments that are not terms. The order of a function is always 1 since it’s arguments are always terms. Examples. In the wff p(x) q(x, p) the order of p is one and the order ...
... The order of a predicate is 1 if its arguments are terms. Otherwise the order is n + 1 where n is the maximum order of the arguments that are not terms. The order of a function is always 1 since it’s arguments are always terms. Examples. In the wff p(x) q(x, p) the order of p is one and the order ...
Slides
... – Standard technique is to index facts with the time when they’re true – This means we have a separate KB for every time point. ...
... – Standard technique is to index facts with the time when they’re true – This means we have a separate KB for every time point. ...
Lecture 11 Artificial Intelligence Predicate Logic
... • Representing knowledge using logic is appealing because you can derive new knowledge from old mathematical deduction. • In this formalism you can conclude that a new statement is true if by proving that it follows from the statement that are already known. • It provides a way of deducing new state ...
... • Representing knowledge using logic is appealing because you can derive new knowledge from old mathematical deduction. • In this formalism you can conclude that a new statement is true if by proving that it follows from the statement that are already known. • It provides a way of deducing new state ...
Exercise
... • Since we assumed nothing about x (other than it is an integer), the argument holds for any integer x. • Therefore, the predicate is TRUE. ...
... • Since we assumed nothing about x (other than it is an integer), the argument holds for any integer x. • Therefore, the predicate is TRUE. ...
Logical Omniscience As Infeasibility - boris
... normal modal logics yields the possibility of using the semantics of Kripke models, which have proved to be a convenient and intuitively clear tool for reasoning about knowledge, based on the Leibnizian supposition of multiple possible worlds. These postulates, however, have an unrealistic consequen ...
... normal modal logics yields the possibility of using the semantics of Kripke models, which have proved to be a convenient and intuitively clear tool for reasoning about knowledge, based on the Leibnizian supposition of multiple possible worlds. These postulates, however, have an unrealistic consequen ...
Uninformed Search
... more existing sentences S. S is called the premise and X the conclusion of the rule. • Proof procedure: a set of inference rules and a procedure of how to use these rules • If X can be generated from S by proof procedure i, we say X is derived from S by i, denoted S |i X, or S | X. • Soundness. An i ...
... more existing sentences S. S is called the premise and X the conclusion of the rule. • Proof procedure: a set of inference rules and a procedure of how to use these rules • If X can be generated from S by proof procedure i, we say X is derived from S by i, denoted S |i X, or S | X. • Soundness. An i ...
The Coinductive Formulation of Common Knowledge
... have made the correct hat choice, they will graduate. Those who make a mistaken choice will be expelled from the school. If you don’t put on a hat, then you will be allowed to try again: you can leave the room and have the chance to make a hat choice and come back. By the way, I want you to know tha ...
... have made the correct hat choice, they will graduate. Those who make a mistaken choice will be expelled from the school. If you don’t put on a hat, then you will be allowed to try again: you can leave the room and have the chance to make a hat choice and come back. By the way, I want you to know tha ...
Propositional Logic Syntax of Propositional Logic
... • checking a set of sentences for satisfiability is NP-complete – but there are some circumstances where the proof only involves a small subset of the KB, so can do some of the work in polynomial time – if a KB is monotonic (i.e., even if we add new sentences to a KB, all the sentences entailed by t ...
... • checking a set of sentences for satisfiability is NP-complete – but there are some circumstances where the proof only involves a small subset of the KB, so can do some of the work in polynomial time – if a KB is monotonic (i.e., even if we add new sentences to a KB, all the sentences entailed by t ...
Group knowledge is not always distributed (neither is it always implicit)
... Theorem 3.3. Let X and Y range over hK1 ,K2 , . . . ,Km ,Gj. Then: £Xw ⇔ £Yw. Theorem 3.3 has, for both the reading as group knowledge as well as that of a receiving agent for G, some remarkable consequences. It implies that the knowledge in the group is nothing else than the knowledge of any partic ...
... Theorem 3.3. Let X and Y range over hK1 ,K2 , . . . ,Km ,Gj. Then: £Xw ⇔ £Yw. Theorem 3.3 has, for both the reading as group knowledge as well as that of a receiving agent for G, some remarkable consequences. It implies that the knowledge in the group is nothing else than the knowledge of any partic ...
Propositional Logic
... – Standard technique is to index facts with the time when they’re true – This means we have a separate KB for every time point. ...
... – Standard technique is to index facts with the time when they’re true – This means we have a separate KB for every time point. ...
HOW FAR WE ARE FROM THE COMPLETE KNOWLEDGE
... because we do not know which of the hypotheses Ei is true. But even if we manage to figure that out, the uncertainty can still remain, because this hypothesis Ei does not necessarily determine uniquely the state of our system. Therefore, if we want to estimate how far we are from the complete knowle ...
... because we do not know which of the hypotheses Ei is true. But even if we manage to figure that out, the uncertainty can still remain, because this hypothesis Ei does not necessarily determine uniquely the state of our system. Therefore, if we want to estimate how far we are from the complete knowle ...
A non-standard Semantics for Inexact Knowledge with Introspection
... standard semantics. Relative to CS, however, necessitation is only frame-valid. Consider, for instance, a model M with three worlds w, w′ , w” such that V (q) = {w, w”} and V (p) = {w′ }, and in which wRw′ and w′ Rw”. Clearly M ²CS ¤p → q but M 2CS ¤(¤p → q). Theorem 2. K45 is complete with respect ...
... standard semantics. Relative to CS, however, necessitation is only frame-valid. Consider, for instance, a model M with three worlds w, w′ , w” such that V (q) = {w, w”} and V (p) = {w′ }, and in which wRw′ and w′ Rw”. Clearly M ²CS ¤p → q but M 2CS ¤(¤p → q). Theorem 2. K45 is complete with respect ...
Deciding Intuitionistic Propositional Logic via Translation into
... So we need to refine our countermodel by adding another knowledge stage w2 refuting a ⇒ b, i.e. w2 a but w2 6 b. However, since by the heredity condition w2 I2 , i.e. w2 (d ⇒ c) ⇒ b we obtain w2 6 d ⇒ c from w2 6 b. Therefore we must add a fourth knowledge stage w3 refuting d ⇒ c, i.e. w3 d but w3 6 ...
... So we need to refine our countermodel by adding another knowledge stage w2 refuting a ⇒ b, i.e. w2 a but w2 6 b. However, since by the heredity condition w2 I2 , i.e. w2 (d ⇒ c) ⇒ b we obtain w2 6 d ⇒ c from w2 6 b. Therefore we must add a fourth knowledge stage w3 refuting d ⇒ c, i.e. w3 d but w3 6 ...
Distributed Knowledge
... The information that a has in w is given by the singleton set f(K; v)g, and the information of b is given by the singleton set f(K; u)g. Since the two worlds are di erent, the intersection of state of a and that of b is empty, and hence, (K; w) j= Dfa;bg?: the distributed knowledge of the two agents ...
... The information that a has in w is given by the singleton set f(K; v)g, and the information of b is given by the singleton set f(K; u)g. Since the two worlds are di erent, the intersection of state of a and that of b is empty, and hence, (K; w) j= Dfa;bg?: the distributed knowledge of the two agents ...
PDF
... ensure that she is talking to B. Both have strong faith in public key encryption and know each other’s public keys. A generates a fresh nonce (a random, previously unused, unguessable number) n and sends it to B encrypted in his public key. When B receives the message, he can indeed decrypt and lear ...
... ensure that she is talking to B. Both have strong faith in public key encryption and know each other’s public keys. A generates a fresh nonce (a random, previously unused, unguessable number) n and sends it to B encrypted in his public key. When B receives the message, he can indeed decrypt and lear ...
Chapter 7
... – P = "person”; M = "mortal”; C = "Confucius" – The above 3 sentences can be roughly represented as: S2: C => P; S1: P => M; S3: C => M. – Then S3 is entailed by S1 and S2 by the chaining rule. ...
... – P = "person”; M = "mortal”; C = "Confucius" – The above 3 sentences can be roughly represented as: S2: C => P; S1: P => M; S3: C => M. – Then S3 is entailed by S1 and S2 by the chaining rule. ...
Critical Terminology for Theory of Knowledge
... Cause and effect: A kind of relation in which one entity or event, called the cause, brings about or helps to bring about another entity or event, called the effect. The proper analysis of cause and effect is a matter of vigorous dispute in philosophy. On most analyses, a cause must exist prior to t ...
... Cause and effect: A kind of relation in which one entity or event, called the cause, brings about or helps to bring about another entity or event, called the effect. The proper analysis of cause and effect is a matter of vigorous dispute in philosophy. On most analyses, a cause must exist prior to t ...
Artificial Intelligence Chapter 4: Knowledge Representation
... propositions (P and Q), if P is true then Q is true. In English, let’s say that P is the proposition “the light is on” and Q is the proposition “the switch is on.” The conditional here can be defined as: if “the light is on” then “the switch is on” ...
... propositions (P and Q), if P is true then Q is true. In English, let’s say that P is the proposition “the light is on” and Q is the proposition “the switch is on.” The conditional here can be defined as: if “the light is on” then “the switch is on” ...
IS COMMON KNOWLEDGE OF RATIONALITY SLUGGISH? 1
... b. Thus, CR ⊆ R ∩ K[{b, 2} × {b}] ⊆ [{2} × {b}]. Therefore, CR is a subset of two disjoint events, and hence CR = ∅. We started with the puzzle that common knowledge of rationality seems to sluggishly follow the full transfinite process of elimination of strongly dominated strategies. We then showed ...
... b. Thus, CR ⊆ R ∩ K[{b, 2} × {b}] ⊆ [{2} × {b}]. Therefore, CR is a subset of two disjoint events, and hence CR = ∅. We started with the puzzle that common knowledge of rationality seems to sluggishly follow the full transfinite process of elimination of strongly dominated strategies. We then showed ...
Uncertainty 99 - Microsoft Research
... the probabilities xi represent an estimation of the respecting rules to be true in the human population. They are not the result of a statistical analysis and so might involve errors. A first trial to solve (3) with these rules shows them to be contradictory. IPF does not converge, there is no distr ...
... the probabilities xi represent an estimation of the respecting rules to be true in the human population. They are not the result of a statistical analysis and so might involve errors. A first trial to solve (3) with these rules shows them to be contradictory. IPF does not converge, there is no distr ...
SP07 cs188 lecture 1..
... All members of a category can be recognized by some properties x (Orange(x) Round(x) Diameter(x)=9.5in MemberOf(x,Balls) MemberOf(x,BasketBalls)) ...
... All members of a category can be recognized by some properties x (Orange(x) Round(x) Diameter(x)=9.5in MemberOf(x,Balls) MemberOf(x,BasketBalls)) ...
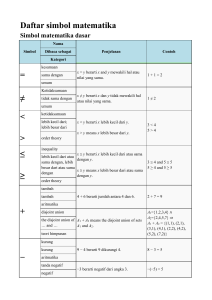
Daftar simbol matematika - Wikipedia bahasa Indonesia
... or join in a lattice or propositional logic, lattice theory exclusive or ...
... or join in a lattice or propositional logic, lattice theory exclusive or ...