MIDTERM 1 : Math 1700 : Spring 2014 SOLUTIONS Problem 1. (5+5
... and it contains f . Therefore there exists g ∈ Q Q Aα ∩ Uα , and consequently g(α0 ) ∈ Aα0 ∩ Uα0 . Hence f (α0 ) ∈ Aα0 . Q Aα , take any basis element Q We now prove the inclusion “⊃”. Given f ∈ Uα in the topology under consideration, which contains f . Then for all indices α, we have: f (α) ∈ Aα ∩ ...
... and it contains f . Therefore there exists g ∈ Q Q Aα ∩ Uα , and consequently g(α0 ) ∈ Aα0 ∩ Uα0 . Hence f (α0 ) ∈ Aα0 . Q Aα , take any basis element Q We now prove the inclusion “⊃”. Given f ∈ Uα in the topology under consideration, which contains f . Then for all indices α, we have: f (α) ∈ Aα ∩ ...
Existence of partitions of unity
... Remark. Some of you may have heard of Urysohn’s metrization theorem which says that any regular second countable topological space is metrizable. Applying this to our manifold M we obtain a metric d that defines the topology (I know of no other place where this metric is in the least bit useful for ...
... Remark. Some of you may have heard of Urysohn’s metrization theorem which says that any regular second countable topological space is metrizable. Applying this to our manifold M we obtain a metric d that defines the topology (I know of no other place where this metric is in the least bit useful for ...
Solution 3
... in M . By premise M is Hausdorff, so these points can be separated by disjoint neighborhoods Vα , α = |G|. T ...
... in M . By premise M is Hausdorff, so these points can be separated by disjoint neighborhoods Vα , α = |G|. T ...
(The Topology of Metric Spaces) (pdf form)
... The Topology of Metric Spaces If (S, d) is a metric space, we let T = TS be the set of open sets of the metric space. The set T is a collection of subsets of S that has the following properties: S (O1) If Ui ∈ T for i ∈ I, then i∈I Ui ∈ T ; (O2) If U, V ∈ T , then U ∩ V ∈ T ; (O3) ∅, S ∈ T . A colle ...
... The Topology of Metric Spaces If (S, d) is a metric space, we let T = TS be the set of open sets of the metric space. The set T is a collection of subsets of S that has the following properties: S (O1) If Ui ∈ T for i ∈ I, then i∈I Ui ∈ T ; (O2) If U, V ∈ T , then U ∩ V ∈ T ; (O3) ∅, S ∈ T . A colle ...
Full text
... three-dimensional Euclidean space as triple products of Fibonacci numbers. This was achieved as a development of two-dimensional ideas involving complex numbers, though the three-dimensional extension was devoid of any dependence on complex numbers. Here, we wish to enlarge these notions to more gen ...
... three-dimensional Euclidean space as triple products of Fibonacci numbers. This was achieved as a development of two-dimensional ideas involving complex numbers, though the three-dimensional extension was devoid of any dependence on complex numbers. Here, we wish to enlarge these notions to more gen ...
Full text
... By Lemma 1, since the common difference in each progression is /!/, it is enough to show that the first term in each progression is a Kronecker number for /!/. When k = 1 the first terms are, respectively, ...
... By Lemma 1, since the common difference in each progression is /!/, it is enough to show that the first term in each progression is a Kronecker number for /!/. When k = 1 the first terms are, respectively, ...
1 - ckw
... 18. The upper-half space En R n , R n T , where T is the usual topology of En , ...
... 18. The upper-half space En R n , R n T , where T is the usual topology of En , ...
DEFINITIONS Math 355 1. For a real number x, the absolute value of
... (d) For all real numbers x and y, |xy| = |x||y|. (e) Let a > 0. Then |x| ≤ a ⇐⇒ −a ≤ x ≤ a and |x| < a ⇐⇒ −a < x < a. (f) For every real number x, −|x| ≤ x ≤ |x|. (g) Triangle Inequality: For all real numbers x and y, |x + y| ≤ |x| + |y| (h) Reverse Triangle Inequality: For all real numbers x and y, ...
... (d) For all real numbers x and y, |xy| = |x||y|. (e) Let a > 0. Then |x| ≤ a ⇐⇒ −a ≤ x ≤ a and |x| < a ⇐⇒ −a < x < a. (f) For every real number x, −|x| ≤ x ≤ |x|. (g) Triangle Inequality: For all real numbers x and y, |x + y| ≤ |x| + |y| (h) Reverse Triangle Inequality: For all real numbers x and y, ...
Math 295. Homework 7 (Due November 5)
... (non-homeomorphic) topologies are there on a three-point set; more precisely, how many three-point topological spaces are there, up to homeomorphism. (2) Non-Standard Topologies on the real line. There are many different notions of “open” for R. We could, in a fit of madness, decide to declare that ...
... (non-homeomorphic) topologies are there on a three-point set; more precisely, how many three-point topological spaces are there, up to homeomorphism. (2) Non-Standard Topologies on the real line. There are many different notions of “open” for R. We could, in a fit of madness, decide to declare that ...
Chapter 4 Euclidean Geometry
... Theorem 4.15 A diagonal of a parallelogram divides it into two congruent triangles. Corrolary 4.16 The opposite sides of a parallelogram are congruent. Opposite angles are also congruent, while adjacent angles are supplementary. We list some properties of parallelograms: 1. If a convex quadrilateral ...
... Theorem 4.15 A diagonal of a parallelogram divides it into two congruent triangles. Corrolary 4.16 The opposite sides of a parallelogram are congruent. Opposite angles are also congruent, while adjacent angles are supplementary. We list some properties of parallelograms: 1. If a convex quadrilateral ...
1 - Ohio State Computer Science and Engineering
... the notation slightly and use a path to both refer to the map γ itself as well as its image γ([0, 1]) ⊂ X in X. Definition 2.1 A topological space X is path connected if for every x, y ∈ X, there is a path connecting them. A topological space X is connected if there does not exist two disjoint non-e ...
... the notation slightly and use a path to both refer to the map γ itself as well as its image γ([0, 1]) ⊂ X in X. Definition 2.1 A topological space X is path connected if for every x, y ∈ X, there is a path connecting them. A topological space X is connected if there does not exist two disjoint non-e ...
geometric congruence
... Note that the criteria listed above are also valid in hyperbolic geometry (and therefore in neutral geometry). Also note that AAS is not valid in spherical geometry, but all of the other criteria are. On the other hand, in both hyperbolic geometry and spherical geometry, AAA is a criterion that indi ...
... Note that the criteria listed above are also valid in hyperbolic geometry (and therefore in neutral geometry). Also note that AAS is not valid in spherical geometry, but all of the other criteria are. On the other hand, in both hyperbolic geometry and spherical geometry, AAA is a criterion that indi ...
All the topological spaces are Hausdorff spaces and all the maps
... such that the two functions α, β defined below are continuous. (1) α : V × V → V is the function of the vector addition α : V × V → V defined by (v, w) 7→ v + w, (2) β is the function of the scalar multiplication β : k × V → V defined by (a, v) 7→ av. Here the two spaces V × V and k × V are equipped ...
... such that the two functions α, β defined below are continuous. (1) α : V × V → V is the function of the vector addition α : V × V → V defined by (v, w) 7→ v + w, (2) β is the function of the scalar multiplication β : k × V → V defined by (a, v) 7→ av. Here the two spaces V × V and k × V are equipped ...
Spherical Geometry Homework
... Given a line AB and a point C on it, there is exactly one point that is antipodal to C: D (think of the North and South Poles). All lines through these polar points are intersecting in two points C and D. Each of these intersecting lines is perpendicular to the line that is the “equator”. Try this o ...
... Given a line AB and a point C on it, there is exactly one point that is antipodal to C: D (think of the North and South Poles). All lines through these polar points are intersecting in two points C and D. Each of these intersecting lines is perpendicular to the line that is the “equator”. Try this o ...
List 6
... 1. Let (X, TX ) and (Y, TY ) be nonempty topological spaces, and let A ⊆ X and B ⊆ Y be proper subsets. If X and Y are connected, show that the complement of (A × B) is connected. 2. Let (X, T) be a topological space, and let (Y, TY ) be a quotient space of X (that is, Y = X/ ∼ for some equivalence ...
... 1. Let (X, TX ) and (Y, TY ) be nonempty topological spaces, and let A ⊆ X and B ⊆ Y be proper subsets. If X and Y are connected, show that the complement of (A × B) is connected. 2. Let (X, T) be a topological space, and let (Y, TY ) be a quotient space of X (that is, Y = X/ ∼ for some equivalence ...
Curves and Manifolds
... Weierstrass's theory of bi-periodic complex analytic functions (cf. elliptic curves, Weierstrass P-function). There are many questions in the theory of plane algebraic curves for which the answer is not known as of the beginning of the 21st century. A differentiable manifold is a type of manifold th ...
... Weierstrass's theory of bi-periodic complex analytic functions (cf. elliptic curves, Weierstrass P-function). There are many questions in the theory of plane algebraic curves for which the answer is not known as of the beginning of the 21st century. A differentiable manifold is a type of manifold th ...
Mathematics Qualifying Exam University of British Columbia September 2, 2010
... 3. Let A be a square matrix with all diagonal entries equal to 2, all entries directly above or below the main diagonal equal to 1, and all other entries equal to 0. Show that every eigenvalue of A is a real number strictly between 0 and 4. ...
... 3. Let A be a square matrix with all diagonal entries equal to 2, all entries directly above or below the main diagonal equal to 1, and all other entries equal to 0. Show that every eigenvalue of A is a real number strictly between 0 and 4. ...
On characterizations of Euclidean spaces
... arbitrarily chosen unit) of the corresponding sector of the unit circle (normalized to 2π). This also defines an angular bisector. ...
... arbitrarily chosen unit) of the corresponding sector of the unit circle (normalized to 2π). This also defines an angular bisector. ...
Lecture 6 outline copy
... a) The triangle inequality guarantees that these balls satisfy the intersection property that is needed to be a basis. b) The topology is Hausdorff (because d(x, y) > 0 unless x = y.) Standard topology on Rn is metric topology. The subspace topology for a subset of a metric space is a metric topolog ...
... a) The triangle inequality guarantees that these balls satisfy the intersection property that is needed to be a basis. b) The topology is Hausdorff (because d(x, y) > 0 unless x = y.) Standard topology on Rn is metric topology. The subspace topology for a subset of a metric space is a metric topolog ...
Lecture 2: Mathematical preliminaries (part 2)
... An expression of a given matrix A in the form of (2.1) is said to be a singular value decomposition of A. The numbers s1 , . . . , sr are called singular values and the vectors x1 , . . . , xr and y1 , . . . , yr are called right and left singular vectors, respectively. The singular values s1 , . . ...
... An expression of a given matrix A in the form of (2.1) is said to be a singular value decomposition of A. The numbers s1 , . . . , sr are called singular values and the vectors x1 , . . . , xr and y1 , . . . , yr are called right and left singular vectors, respectively. The singular values s1 , . . ...
LOYOLA COLLEGE (AUTONOMOUS), CHENNAI LOYOLA COLLEGE (AUTONOMOUS), CHENNAI – 600 034
... 14.) Let V and W be two n-dimensional vector spaces over . Then prove that any isomorphism T of V onto W maps a basis of V onto basis of W. 15.) Prove that for any two vectors , ...
... 14.) Let V and W be two n-dimensional vector spaces over . Then prove that any isomorphism T of V onto W maps a basis of V onto basis of W. 15.) Prove that for any two vectors , ...
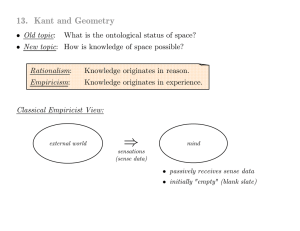
13.Kant and Geometry
... "The apodeictic certainty of all geometrical propositions, and the possibility of their a priori construction, is grounded in this a priori necessity of space. Were this representation of space a concept acquired a posteriori, and derived from outer experience in general, the first principles of mat ...
... "The apodeictic certainty of all geometrical propositions, and the possibility of their a priori construction, is grounded in this a priori necessity of space. Were this representation of space a concept acquired a posteriori, and derived from outer experience in general, the first principles of mat ...
Euclidean space
In geometry, Euclidean space encompasses the two-dimensional Euclidean plane, the three-dimensional space of Euclidean geometry, and certain other spaces. It is named after the Ancient Greek mathematician Euclid of Alexandria. The term ""Euclidean"" distinguishes these spaces from other types of spaces considered in modern geometry. Euclidean spaces also generalize to higher dimensions.Classical Greek geometry defined the Euclidean plane and Euclidean three-dimensional space using certain postulates, while the other properties of these spaces were deduced as theorems. Geometric constructions are also used to define rational numbers. When algebra and mathematical analysis became developed enough, this relation reversed and now it is more common to define Euclidean space using Cartesian coordinates and the ideas of analytic geometry. It means that points of the space are specified with collections of real numbers, and geometric shapes are defined as equations and inequalities. This approach brings the tools of algebra and calculus to bear on questions of geometry and has the advantage that it generalizes easily to Euclidean spaces of more than three dimensions.From the modern viewpoint, there is essentially only one Euclidean space of each dimension. With Cartesian coordinates it is modelled by the real coordinate space (Rn) of the same dimension. In one dimension, this is the real line; in two dimensions, it is the Cartesian plane; and in higher dimensions it is a coordinate space with three or more real number coordinates. Mathematicians denote the n-dimensional Euclidean space by En if they wish to emphasize its Euclidean nature, but Rn is used as well since the latter is assumed to have the standard Euclidean structure, and these two structures are not always distinguished. Euclidean spaces have finite dimension.