figure 6-2 - JSNE Group
... • Every time tail of a node considered – List size reduced by one – Eventually list size reduced to zero – Recursion stops ...
... • Every time tail of a node considered – List size reduced by one – Eventually list size reduced to zero – Recursion stops ...
Java Software Structures, 4th Edition Exercise Solutions, Ch. 8
... Write a recursive method to reverse a string. Explain why you would not normally use recursion to solve this problem. public String reverse (String text) ...
... Write a recursive method to reverse a string. Explain why you would not normally use recursion to solve this problem. public String reverse (String text) ...
Set Theory II
... Last time we discussed the Axioms of Extension, Specification, Unordered Pairs, and Unions. Some more aioms of set theory Powers For each set there exists a collection of sets that contains among its elements all the subsets of the given set. (Combined with the Axiom of Specification, it follows tha ...
... Last time we discussed the Axioms of Extension, Specification, Unordered Pairs, and Unions. Some more aioms of set theory Powers For each set there exists a collection of sets that contains among its elements all the subsets of the given set. (Combined with the Axiom of Specification, it follows tha ...
Introduction to "Mathematical Foundations for Software Engineering"
... Since then, many computational models – including some very simple models - have been shown to be computationally equivalent to the Turing machine; such models are said to be Turing complete. Computability is the study of the limits of these machines 2012: J Paul Gibson ...
... Since then, many computational models – including some very simple models - have been shown to be computationally equivalent to the Turing machine; such models are said to be Turing complete. Computability is the study of the limits of these machines 2012: J Paul Gibson ...
Recursion
... "One Small Step/Complete the Solution" • Each invocation of a recursive function performs one small step towards the entire solution and makes a recursive call to complete the solution. ...
... "One Small Step/Complete the Solution" • Each invocation of a recursive function performs one small step towards the entire solution and makes a recursive call to complete the solution. ...
PDF
... first-order logic to the decidability problem for theories that can represent the computable functions, provided we find a finitely axiomatizable theory that has this property. Since the theories we considered so far are not finitely axiomatizable, we postpone the proof of Church’s undecidability th ...
... first-order logic to the decidability problem for theories that can represent the computable functions, provided we find a finitely axiomatizable theory that has this property. Since the theories we considered so far are not finitely axiomatizable, we postpone the proof of Church’s undecidability th ...
Constructive Set Theory and Brouwerian Principles1
... In what follows we shall use the notions of proof-theoretic equivalence of theories and proof-theoretic strength of a theory whose precise definitions one can find in [18]. For our purposes here we take proof-theoretic equivalence of set theories T1 and T2 to mean that these theories prove the same ...
... In what follows we shall use the notions of proof-theoretic equivalence of theories and proof-theoretic strength of a theory whose precise definitions one can find in [18]. For our purposes here we take proof-theoretic equivalence of set theories T1 and T2 to mean that these theories prove the same ...
pdf
... i.e. if the characteristic function of that set is computable. (4) T is called axiomatizable, if there is a decidable subset of T whose logical consequences are exactly the theorems of T . T is finitely axiomatizable if it is axiomatizable with a finite set of axioms. (5) A set S ⊆N is called defina ...
... i.e. if the characteristic function of that set is computable. (4) T is called axiomatizable, if there is a decidable subset of T whose logical consequences are exactly the theorems of T . T is finitely axiomatizable if it is axiomatizable with a finite set of axioms. (5) A set S ⊆N is called defina ...
A simple proof of Parsons` theorem
... ago, Charles Parsons showed that the provably total functions of IΣ1 are exactly the primitive recursive functions. In this paper, we observe that Parsons’ result is a consequence of Herbrand’s theorem concerning the ∃∀∃-consequences of universal theories. We give a self-contained proof requiring on ...
... ago, Charles Parsons showed that the provably total functions of IΣ1 are exactly the primitive recursive functions. In this paper, we observe that Parsons’ result is a consequence of Herbrand’s theorem concerning the ∃∀∃-consequences of universal theories. We give a self-contained proof requiring on ...
PDF hosted at the Radboud Repository of the Radboud University
... can be obtained, starting in such a small initial configuration. The particular game and its Ackermann function like behavior were already well-known. My contribution mainly restricted to some investigations for small initial configurations, the formulation of the problem and passing it to the sourc ...
... can be obtained, starting in such a small initial configuration. The particular game and its Ackermann function like behavior were already well-known. My contribution mainly restricted to some investigations for small initial configurations, the formulation of the problem and passing it to the sourc ...
This paper consists of two parts both of which attempt to provide
... and Sn be Rn0 / ∼ and Sn0 / ∼ respectively. The tautologies considered express that there is a sequence of n-tuples u1 , . . . , un such that for any n-tuples x and y either ¬Rn (u1 / ∼, u2 / ∼, y/ ∼) or for some ui , Sn (ui / ∼, x/ ∼). The result is, again, if there is any g as above which is expo ...
... and Sn be Rn0 / ∼ and Sn0 / ∼ respectively. The tautologies considered express that there is a sequence of n-tuples u1 , . . . , un such that for any n-tuples x and y either ¬Rn (u1 / ∼, u2 / ∼, y/ ∼) or for some ui , Sn (ui / ∼, x/ ∼). The result is, again, if there is any g as above which is expo ...
Friendly Logics, Fall 2015, Homework 1
... (a) Prove that the statement of the Soundness Theorem (3.1) is equivalent to the following statement: for any ⌃ if ⌃ is satisfiable then it is consistent. (b) Prove that the statement of the Compleness Theorem (3.3) is equivalent to the following statement: for any ⌃ if ⌃ is consistent then it is sa ...
... (a) Prove that the statement of the Soundness Theorem (3.1) is equivalent to the following statement: for any ⌃ if ⌃ is satisfiable then it is consistent. (b) Prove that the statement of the Compleness Theorem (3.3) is equivalent to the following statement: for any ⌃ if ⌃ is consistent then it is sa ...
Recursion
... procedure itself. A procedure that goes through recursion is said to be 'recursive'. To understand recursion, one must recognize the distinction between a procedure and the running of a procedure. A procedure is a set of steps that are to be taken based on a set of rules. The running of a procedure ...
... procedure itself. A procedure that goes through recursion is said to be 'recursive'. To understand recursion, one must recognize the distinction between a procedure and the running of a procedure. A procedure is a set of steps that are to be taken based on a set of rules. The running of a procedure ...
We showed on Tuesday that Every relation in the arithmetical
... Gödel’s First Incompleteness Theorem essentially states that no reasonable axiom system can “capture” all arithmetic truth , because the set True is not semidecidable. To illustrate the theorem we need some definitions and observations. ...
... Gödel’s First Incompleteness Theorem essentially states that no reasonable axiom system can “capture” all arithmetic truth , because the set True is not semidecidable. To illustrate the theorem we need some definitions and observations. ...
Lecture 5: 9/11/98
... • We now prove REC is closed under two set operations – Set Complement – Set Intersection ...
... • We now prove REC is closed under two set operations – Set Complement – Set Intersection ...
Theories.Axioms,Rules of Inference
... concerns a given theory in a given logic. That theory is a set of axioms. The logic has rules of inference that allow us to generate other theorems from those axioms. (Axioms are theorems.) When we start ACL2, it has lots of functions already defined and it correspondingly has axioms for those funct ...
... concerns a given theory in a given logic. That theory is a set of axioms. The logic has rules of inference that allow us to generate other theorems from those axioms. (Axioms are theorems.) When we start ACL2, it has lots of functions already defined and it correspondingly has axioms for those funct ...
PDF
... them intuitively. Moreover, we will see more deeply that this is not an entirely adequate way to understand numbers, even with the constructive semantics of HA. We already know that the very simple theory Q is too weak. This is quite easy to see. We noted in Lecture 11 that we need some form of indu ...
... them intuitively. Moreover, we will see more deeply that this is not an entirely adequate way to understand numbers, even with the constructive semantics of HA. We already know that the very simple theory Q is too weak. This is quite easy to see. We noted in Lecture 11 that we need some form of indu ...
DUBLIN CITY UNIVERSITY
... In the context of Complexity, what is meant by polynomial-time reducibility? Prove that if L1 ∈ P and L1 is polynomially reducible to L2 , then L2 ∈ P . [End of Question 5] ...
... In the context of Complexity, what is meant by polynomial-time reducibility? Prove that if L1 ∈ P and L1 is polynomially reducible to L2 , then L2 ∈ P . [End of Question 5] ...
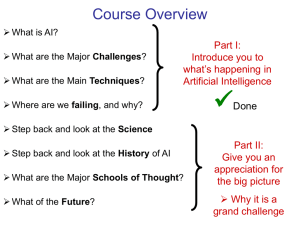
Step back and look at the Science
... Gottfried Wilhelm Leibniz (1646 - 1716) Believed that much of human reasoning could be reduced to mathematical calculations Believed in calculations using symbols He wanted a symbol for each fundamental concept Complex concepts would be built by combining fundamentals Thought of an “algeb ...
... Gottfried Wilhelm Leibniz (1646 - 1716) Believed that much of human reasoning could be reduced to mathematical calculations Believed in calculations using symbols He wanted a symbol for each fundamental concept Complex concepts would be built by combining fundamentals Thought of an “algeb ...
ppt - Dr. Wissam Fawaz
... Sum of values from 1 to N (ctd) // This method returns the sum of 1 to num // Refer to SumApp project ...
... Sum of values from 1 to N (ctd) // This method returns the sum of 1 to num // Refer to SumApp project ...
HW 12
... 4. The difference between two sets A and B is the set of all objects that belong to set A but not to B. This is written as A \ B a. Provide a definitional axiom for A \ B (use a 2-place function symbol diff(x,y)) b. Construct a formal proof that shows that for any sets A, B, and C: A (B \ C) = (A ...
... 4. The difference between two sets A and B is the set of all objects that belong to set A but not to B. This is written as A \ B a. Provide a definitional axiom for A \ B (use a 2-place function symbol diff(x,y)) b. Construct a formal proof that shows that for any sets A, B, and C: A (B \ C) = (A ...
notes
... Let P be a propositions containing the (distinct) atomic formulas A 1 , . . . , An and v1 , . . . v2n its interpretations. We denote with v P the boolean function associated with P , i.e. vP : {0, 1}n → {0, 1} is defined as follows: for each (a 1 , . . . , an ), ai ∈ {0, 1}, there exists i ∈ {1, . ...
... Let P be a propositions containing the (distinct) atomic formulas A 1 , . . . , An and v1 , . . . v2n its interpretations. We denote with v P the boolean function associated with P , i.e. vP : {0, 1}n → {0, 1} is defined as follows: for each (a 1 , . . . , an ), ai ∈ {0, 1}, there exists i ∈ {1, . ...
CS112 Lecture: Recursion Last revised 3/20/08 1. Von Koch curve images
... a) Base case: a constant, by itself, is an arithmetic expression. Example: 3 is an arithmetic expression. b) Another base case: a variable, by itself, is an arithmetic expression. Example: X is an arithmetic expression. c) Recursive case: the negation of an arithmetic expression, enclosed in parenth ...
... a) Base case: a constant, by itself, is an arithmetic expression. Example: 3 is an arithmetic expression. b) Another base case: a variable, by itself, is an arithmetic expression. Example: X is an arithmetic expression. c) Recursive case: the negation of an arithmetic expression, enclosed in parenth ...