Slide 1
... ● There is always a next configuration of M and thus a next row in the tiling iff M does not halt. ● T is in TILES iff there is always a next row. ● So if it were possible to semidecide whether T is in TILES it would be possible to semidecide whether M fails to halt on . But H is not in SD. So ne ...
... ● There is always a next configuration of M and thus a next row in the tiling iff M does not halt. ● T is in TILES iff there is always a next row. ● So if it were possible to semidecide whether T is in TILES it would be possible to semidecide whether M fails to halt on . But H is not in SD. So ne ...
Document
... The more fruitful type of definition is a matter of drawing boundary lines that were not previously given at all. What we shall be able to infer from it, cannot be inspected in advance; here, we are not simply taking out of the box again what we have just put into it. The conclusions we draw from i ...
... The more fruitful type of definition is a matter of drawing boundary lines that were not previously given at all. What we shall be able to infer from it, cannot be inspected in advance; here, we are not simply taking out of the box again what we have just put into it. The conclusions we draw from i ...
Ordered Groups: A Case Study In Reverse Mathematics 1 Introduction
... The fundamental question in reverse mathematics is to determine which set existence axioms are required to prove particular theorems of mathematics. In addition to being interesting in their own right, answers to this question have consequences in both effective mathematics and the foundations of ma ...
... The fundamental question in reverse mathematics is to determine which set existence axioms are required to prove particular theorems of mathematics. In addition to being interesting in their own right, answers to this question have consequences in both effective mathematics and the foundations of ma ...
Arithmetic as a theory modulo
... The setting, however, is different. Definition 3 (Reducibility candidates). A proof-term is said to be neutral if it is a proof variable or an elimination (i.e. of the form (π π 0 ), fst(π), snd (π), δ(π1 , απ2 , βπ3 ), δ⊥ (π), (π t), δ∃ (π, xαπ 0 )), but not an introduction. A set R of proof-terms ...
... The setting, however, is different. Definition 3 (Reducibility candidates). A proof-term is said to be neutral if it is a proof variable or an elimination (i.e. of the form (π π 0 ), fst(π), snd (π), δ(π1 , απ2 , βπ3 ), δ⊥ (π), (π t), δ∃ (π, xαπ 0 )), but not an introduction. A set R of proof-terms ...
Semi-constr. theories - Stanford Mathematics
... result being of type τ. Application in terms such as rst is read by association to the left, while the t.s. ρ → σ → τ is read by association to the right. Each higher type symbol σ can be written in the form σ = (σ1 → … → σk → 0 ); then equality s = t at type σ is regarded as an abbreviation for sx1 ...
... result being of type τ. Application in terms such as rst is read by association to the left, while the t.s. ρ → σ → τ is read by association to the right. Each higher type symbol σ can be written in the form σ = (σ1 → … → σk → 0 ); then equality s = t at type σ is regarded as an abbreviation for sx1 ...
Slide 1
... • Given a positive integer n, factorial is defined as the product of all integers between n an1. i.e focatorial of 4 is 4*3*2*1=24 • Hence we have the formula n!=1 if n==0 n!=n*(n-1)*(n-2)….1 if(n>0) • We can see that n!=n*(n-1)!. If we go further, n!=n*(n1)*(n-2)!. This can continue until 0 is enco ...
... • Given a positive integer n, factorial is defined as the product of all integers between n an1. i.e focatorial of 4 is 4*3*2*1=24 • Hence we have the formula n!=1 if n==0 n!=n*(n-1)*(n-2)….1 if(n>0) • We can see that n!=n*(n-1)!. If we go further, n!=n*(n1)*(n-2)!. This can continue until 0 is enco ...
Mixed Recursion: Sec. 8.4
... If you can show that the formula works for a specific case, and that if it works for one natural number it will work for the next natural number, then you have proven that the formula will work for all natural numbers. ...
... If you can show that the formula works for a specific case, and that if it works for one natural number it will work for the next natural number, then you have proven that the formula will work for all natural numbers. ...
Recursion
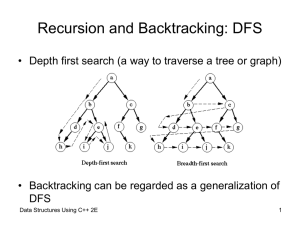
... • Learn about recursive definitions • Explore the base case and the general case of a recursive definition • Discover what a recursive algorithm is • Learn about recursive methods • Explore how to use recursive methods to implement recursive algorithms • Learn how recursion implements backtracking ...
... • Learn about recursive definitions • Explore the base case and the general case of a recursive definition • Discover what a recursive algorithm is • Learn about recursive methods • Explore how to use recursive methods to implement recursive algorithms • Learn how recursion implements backtracking ...
If T is a consistent theory in the language of arithmetic, we say a set
... if a prime divides a product it divides one of its factors, and that if two numbers with no common prime factor both divide a number, then so does their product. (The reader may recognize these as results we took for granted in the proof of Lemma 16.5.) Once we have enough elementary lemmas, we can ...
... if a prime divides a product it divides one of its factors, and that if two numbers with no common prime factor both divide a number, then so does their product. (The reader may recognize these as results we took for granted in the proof of Lemma 16.5.) Once we have enough elementary lemmas, we can ...
ON THE QUOTIENT STRUCTURE OF COMPUTABLY
... we want to put elements into either A or B but not both. It is worth mentioning that being able to put elements into one side makes our strategy different from the usual noncuppable strategy. – If w enters K for some w < j, then we initialize the N strategy. A crude analysis of the impact of the rev ...
... we want to put elements into either A or B but not both. It is worth mentioning that being able to put elements into one side makes our strategy different from the usual noncuppable strategy. – If w enters K for some w < j, then we initialize the N strategy. A crude analysis of the impact of the rev ...
The Diagonal Lemma Fails in Aristotelian Logic
... truth of what is said, but of its being either true or false.” [Original italics] (Strawson, p. 174) We will, however, do one better and take the entire (∃x)Fx & (Ex)~Gx as the presupposition. Then A is neither true nor false if (∃x)Fx & (∃x)~Gx is not true. For our purposes it is important to note ...
... truth of what is said, but of its being either true or false.” [Original italics] (Strawson, p. 174) We will, however, do one better and take the entire (∃x)Fx & (Ex)~Gx as the presupposition. Then A is neither true nor false if (∃x)Fx & (∃x)~Gx is not true. For our purposes it is important to note ...
Computational foundations of basic recursive function theory
... become simpler, and many of the central concepts become more abstract. In this approach computations are viewed as mathematical objects, and theorems in recursion theory may be classified according to which axioms of computation are needed to prove them. The theory is about typed functions over the ...
... become simpler, and many of the central concepts become more abstract. In this approach computations are viewed as mathematical objects, and theorems in recursion theory may be classified according to which axioms of computation are needed to prove them. The theory is about typed functions over the ...
Induction and Recursion 093 ICS 253: Discrete
... • In recursively defined sets, the basis step defines some initial elements and the recursive step defines a rule for constructing new elements from those already in the set. • Recursive definitions may also include an exclusion rule, which specifies that a recursively defined set contains nothing o ...
... • In recursively defined sets, the basis step defines some initial elements and the recursive step defines a rule for constructing new elements from those already in the set. • Recursive definitions may also include an exclusion rule, which specifies that a recursively defined set contains nothing o ...
Jean Van Heijenoort`s View of Modern Logic
... Thank you very much for your friendly card and the offprints of your papers. I am concurrently sending you reprints of my two essays regarding the fundamentals; several passages therein relate to the results that you obtained. For example, my paper entitled “Über formal unentscheidbare Sätze etc.” ...
... Thank you very much for your friendly card and the offprints of your papers. I am concurrently sending you reprints of my two essays regarding the fundamentals; several passages therein relate to the results that you obtained. For example, my paper entitled “Über formal unentscheidbare Sätze etc.” ...
On the completeness of the equations for the Kleene star in bisimulation
... the recent handbook chapter of Baeten and Verhoef [6], but its proof was omitted because it was considered beyond the scope of that paper. Here, a simpler completeness proof is proposed, which is based on induction on the structure of process terms. This proof is better suited for presentation in a ...
... the recent handbook chapter of Baeten and Verhoef [6], but its proof was omitted because it was considered beyond the scope of that paper. Here, a simpler completeness proof is proposed, which is based on induction on the structure of process terms. This proof is better suited for presentation in a ...
Automata and formal languages ∗
... ways to compute or to show that they don’t exist. A closely related problem is still unsolved: what is the minimal value of the star-height of extended rational expressions, namely those allowing the additional use of the complementation? No example could yet be proved to have extended star-height m ...
... ways to compute or to show that they don’t exist. A closely related problem is still unsolved: what is the minimal value of the star-height of extended rational expressions, namely those allowing the additional use of the complementation? No example could yet be proved to have extended star-height m ...
mass problems associated with effectively closed sets
... simplicial complexes, the diffeomorphism problem for compact manifolds, and the problem of integrability in elementary terms. In an influential 1954 paper [56], Kleene and Post introduced a scheme for classifying unsolvable mathematical problems. Informally, by a real we mean a point in an effective ...
... simplicial complexes, the diffeomorphism problem for compact manifolds, and the problem of integrability in elementary terms. In an influential 1954 paper [56], Kleene and Post introduced a scheme for classifying unsolvable mathematical problems. Informally, by a real we mean a point in an effective ...
part_3
... void pre-order(node& root) if (root != NULL) { visit(root); // do something pre-order(root->left ); pre-order(root->right); ...
... void pre-order(node& root) if (root != NULL) { visit(root); // do something pre-order(root->left ); pre-order(root->right); ...
full text (.pdf)
... history of M on some input, it halts immediately. It also halts if it ever encounters a halting state of M anywhere in the string. Thus the only Herbrand model of T0 that would cause p not to halt is the one describing the infinite valid computation history of M on x in the case that M does not halt ...
... history of M on some input, it halts immediately. It also halts if it ever encounters a halting state of M anywhere in the string. Thus the only Herbrand model of T0 that would cause p not to halt is the one describing the infinite valid computation history of M on x in the case that M does not halt ...
Beautifying Gödel - Department of Computer Science
... shall not do so. Statement (g) says that NT is consistent. The false statement (m) says that NT is complete. We included division in NT to give a simple sentence that is neither a theorem nor an antitheorem; Gödel's surprise result was that, even without division, with only addition and multiplicati ...
... shall not do so. Statement (g) says that NT is consistent. The false statement (m) says that NT is complete. We included division in NT to give a simple sentence that is neither a theorem nor an antitheorem; Gödel's surprise result was that, even without division, with only addition and multiplicati ...
The Complexity of Local Stratification - SUrface
... Definition 2.2: Let f be a unary partial recursive function on the natural numbers. 2-register machine M computes f if for every natural number a: M, when started at instruction 1 with X1 = 2a, X2 = 0 halts (by passing control to the nonexistent (n + 1)st instruction) with X1 = 2f(a) ·and X2 = 0 if ...
... Definition 2.2: Let f be a unary partial recursive function on the natural numbers. 2-register machine M computes f if for every natural number a: M, when started at instruction 1 with X1 = 2a, X2 = 0 halts (by passing control to the nonexistent (n + 1)st instruction) with X1 = 2f(a) ·and X2 = 0 if ...
Some Applications of Logic to Feasibility in Higher Types
... 1 which are just the basic feasible functionals. Our argument for i = 1 easily generalises to S i2 and P i for any i. 1.4 Proof Techniques The main novelty of this paper is in the way we use logic (in particular formal theories) as a tool to derive results of recursion-theoretic nature as well as re ...
... 1 which are just the basic feasible functionals. Our argument for i = 1 easily generalises to S i2 and P i for any i. 1.4 Proof Techniques The main novelty of this paper is in the way we use logic (in particular formal theories) as a tool to derive results of recursion-theoretic nature as well as re ...
CA320 - Computability & Complexity Overview
... If x ∈ A and y ∈ B, then xRy is true if (x, y ) ∈ R. A function is a special kind of relationship in which an element of the domain to related to just one element of the codomain. A function f : A → B relates an element x ∈ A to an element y ∈ B where y = f (x). If f (x) is defined for all x ∈ A the ...
... If x ∈ A and y ∈ B, then xRy is true if (x, y ) ∈ R. A function is a special kind of relationship in which an element of the domain to related to just one element of the codomain. A function f : A → B relates an element x ∈ A to an element y ∈ B where y = f (x). If f (x) is defined for all x ∈ A the ...