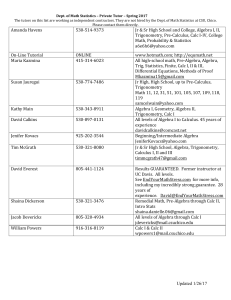
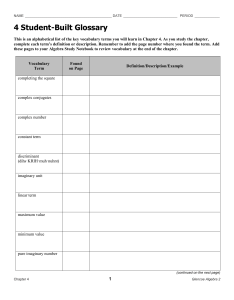
on torsion-free abelian groups and lie algebras
... that D is a locally algebraic derivation. By Theorem 2, D = Ry+Dd, where Rv is the right multiplication by y = 2ZT ayuy, lor some y and d. Suppose that some nonzero 7 is y-admissible. We may simply order G in such a way that this 7>0. Call u( the leading term in an element 2 of L(G, g, f) if e is th ...
... that D is a locally algebraic derivation. By Theorem 2, D = Ry+Dd, where Rv is the right multiplication by y = 2ZT ayuy, lor some y and d. Suppose that some nonzero 7 is y-admissible. We may simply order G in such a way that this 7>0. Call u( the leading term in an element 2 of L(G, g, f) if e is th ...
3.2 Adding and Subtracting Polynomials
... additive inverses of each other. When put together, they model zero. ...
... additive inverses of each other. When put together, they model zero. ...
Find Inverse Switch X and Y Notes
... Functions and Their Inverses Check It Out! Example 2 Continued ...
... Functions and Their Inverses Check It Out! Example 2 Continued ...
The Heisenberg Algebra
... for most purposes in physics just the Lie algebra relations are needed. It was first defined by Weyl and physicists often refer to it as the “Weyl group”, but that name is already taken among mathematicians as we have seen. We can exponentiate using the Baker-Campbell-Hausdorff formula (which simpli ...
... for most purposes in physics just the Lie algebra relations are needed. It was first defined by Weyl and physicists often refer to it as the “Weyl group”, but that name is already taken among mathematicians as we have seen. We can exponentiate using the Baker-Campbell-Hausdorff formula (which simpli ...
EXAMPLE SHEET 3 1. Let A be a k-linear category, for a
... satisfies ei pej q “ δij . Prove that i“1 ei b ei P V b V is independent of the choice of the basis of V . 3. Let k be a field and Mn pkq the algebra of n ˆ n matrices with entries in k, and denote by OpMn pkqq be the free commutative algebra on the variables tXij : 1 ď i, j ď nu (ie the plynomial a ...
... satisfies ei pej q “ δij . Prove that i“1 ei b ei P V b V is independent of the choice of the basis of V . 3. Let k be a field and Mn pkq the algebra of n ˆ n matrices with entries in k, and denote by OpMn pkqq be the free commutative algebra on the variables tXij : 1 ď i, j ď nu (ie the plynomial a ...