Math 261y: von Neumann Algebras (Lecture 1)
... Passing from the group G to the von Neumann algebra of a representation α : G → B(V ) generally loses a great deal of information. However, it retains the information we are interested in: namely, the structure of all G-equivariant direct sum decompositions of G. Moreover, the von Neumann algebra o ...
... Passing from the group G to the von Neumann algebra of a representation α : G → B(V ) generally loses a great deal of information. However, it retains the information we are interested in: namely, the structure of all G-equivariant direct sum decompositions of G. Moreover, the von Neumann algebra o ...
Real Composition Algebras by Steven Clanton
... binary (rank 2) quadratic forms. In particular, Gauss proved that any positive definite binary quadratic form can be linearly transformed into the two-squares formula w12 + w22 = (u21 + u22 ) (v12 + v22 ). This shows not only the existence of an algebra for every form but also an isomorphism to the ...
... binary (rank 2) quadratic forms. In particular, Gauss proved that any positive definite binary quadratic form can be linearly transformed into the two-squares formula w12 + w22 = (u21 + u22 ) (v12 + v22 ). This shows not only the existence of an algebra for every form but also an isomorphism to the ...
Lecture Notes for Section 8.5 (More Simplifying and Operations with
... Big Idea: It is customary with rational expressions to not have radicals in the denominator. To “get rid of” a sum of square roots in the denominator, multiply top and bottom by the conjugate of the denominator. Criteria for a Simplified Radical Expression: ...
... Big Idea: It is customary with rational expressions to not have radicals in the denominator. To “get rid of” a sum of square roots in the denominator, multiply top and bottom by the conjugate of the denominator. Criteria for a Simplified Radical Expression: ...
THE DIRAC OPERATOR 1. First properties 1.1. Definition. Let X be a
... We also note that the symbol of D2 is therefore given on (v, t) by ktk2 v, and this is precisely the symbol of a Laplacian-type operator. The Dirac operator can be thought of (and was originally introduced) as a square root for the Laplacian. There are a few further natural conditions to impose here ...
... We also note that the symbol of D2 is therefore given on (v, t) by ktk2 v, and this is precisely the symbol of a Laplacian-type operator. The Dirac operator can be thought of (and was originally introduced) as a square root for the Laplacian. There are a few further natural conditions to impose here ...
AN EXAMPLE OF A COQUECIGRUE EMBEDDED IN R Fausto Ongay
... We easily see from here that G1 and Gi are closed under both operations; moreover, the bar unit 1 belongs to both, so they are subdigroups of G. Also clearly none of them is trivial, in the sense that they are not Lie groups. As a group R+ is isomorphic to R via the logarithm, therefore, for G1 , wh ...
... We easily see from here that G1 and Gi are closed under both operations; moreover, the bar unit 1 belongs to both, so they are subdigroups of G. Also clearly none of them is trivial, in the sense that they are not Lie groups. As a group R+ is isomorphic to R via the logarithm, therefore, for G1 , wh ...
quadratic equation
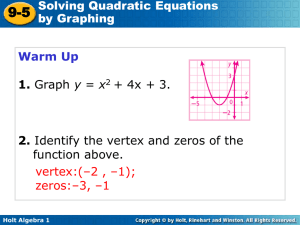
... equation. A quadratic equation is an equation that can be written in the standard form ax2 + bx + c = 0, where a, b, and c are real numbers and a ≠ 0. When writing a quadratic function as its related quadratic equation, you replace y with 0. So y = 0. y = ax2 + bx + c 0 = ax2 + bx + c ax2 + bx + c = ...
... equation. A quadratic equation is an equation that can be written in the standard form ax2 + bx + c = 0, where a, b, and c are real numbers and a ≠ 0. When writing a quadratic function as its related quadratic equation, you replace y with 0. So y = 0. y = ax2 + bx + c 0 = ax2 + bx + c ax2 + bx + c = ...
linear representations as modules for the group ring
... A routine verification proves the following: Proposition 4.3. The natural injection G → kG has the following properties: (1) It identifies G as a subgroup of the group of units of kG. (2) Its image spans k-linearly the group ring. (3) Given an associative k-algebra A with identity and a homomorphism ...
... A routine verification proves the following: Proposition 4.3. The natural injection G → kG has the following properties: (1) It identifies G as a subgroup of the group of units of kG. (2) Its image spans k-linearly the group ring. (3) Given an associative k-algebra A with identity and a homomorphism ...


















![arXiv:math/9912226v1 [math.QA] 29 Dec 1999](http://s1.studyres.com/store/data/016499604_1-20cde5c97e19d73a25fd6a9497507102-300x300.png)