Practice Final
... 7. Find a, b, c such that y = a2 + b cos 2x + c sin 3x is the least square approximation to y = x in [−π, π] with respect to the weight function w(x) = 1. 8. Derive the nonlinear system for a, b such that the exponential function y = beax fit the following data points, (1.0, 1.0), (1.2, 1.4), (1.5, ...
... 7. Find a, b, c such that y = a2 + b cos 2x + c sin 3x is the least square approximation to y = x in [−π, π] with respect to the weight function w(x) = 1. 8. Derive the nonlinear system for a, b such that the exponential function y = beax fit the following data points, (1.0, 1.0), (1.2, 1.4), (1.5, ...
URL Address
... • ode113 is a variable order Adams-Bashforth-Moulton PECE solver. It may be more efficient than ode45 at stringent tolerances and when the ODE file function is particularly expensive to evaluate. ode113 is a multistep s olver - it normally needs the solutions at several preceding time points to comp ...
... • ode113 is a variable order Adams-Bashforth-Moulton PECE solver. It may be more efficient than ode45 at stringent tolerances and when the ODE file function is particularly expensive to evaluate. ode113 is a multistep s olver - it normally needs the solutions at several preceding time points to comp ...
Curve Fitting - Ecs.csus.edu
... Cubic splines • Polynomial approximation can produce points that are not allowed • For example, if the data is for absolute voltage, polynomial can have negative and positive values • Splines are piecewise approximating cubic functions that can overcome polynomial problems ...
... Cubic splines • Polynomial approximation can produce points that are not allowed • For example, if the data is for absolute voltage, polynomial can have negative and positive values • Splines are piecewise approximating cubic functions that can overcome polynomial problems ...
Final Exam: 15-853Algorithm in the real and virtual world
... B) No. If there were two distinct paths between a source (positive b) and sink (negative b) with nonzero flow, there would be a cycle starting from b and back to b would. C) In terms of the graph, one step of the simplex method corresponds to one step of generating a minimum spanning tree: add an ed ...
... B) No. If there were two distinct paths between a source (positive b) and sink (negative b) with nonzero flow, there would be a cycle starting from b and back to b would. C) In terms of the graph, one step of the simplex method corresponds to one step of generating a minimum spanning tree: add an ed ...
A Randomized Approximate Nearest Neighbors
... Given a collection of n points x1 , x2 , . . . , xn in Rd and an integer k << n, the task of finding the k nearest neighbors for each xi is known as the “Nearest Neighbors Problem”; it is ubiquitous in a number of areas of Computer Science: Machine Learning, Data Mining, Artificial Intelligence, etc ...
... Given a collection of n points x1 , x2 , . . . , xn in Rd and an integer k << n, the task of finding the k nearest neighbors for each xi is known as the “Nearest Neighbors Problem”; it is ubiquitous in a number of areas of Computer Science: Machine Learning, Data Mining, Artificial Intelligence, etc ...
Stationary Schrödinger equation (1.5 LP) Vibrational states of a HCl
... Given a single HCl molecule, in harmonic approximation the potential of the system can be described by: ...
... Given a single HCl molecule, in harmonic approximation the potential of the system can be described by: ...
Study Guide for Exam 1.
... Theorem for Integrals, Rolle’s Theorem, the Intermediate Value Theorem, and Taylor’s Theorem with error term. Review all of these theorems and know when they can be applied. 2. Iterative Methods for One Dimensional Problems: Understand how and why the bisection method works. Know the fixed point ite ...
... Theorem for Integrals, Rolle’s Theorem, the Intermediate Value Theorem, and Taylor’s Theorem with error term. Review all of these theorems and know when they can be applied. 2. Iterative Methods for One Dimensional Problems: Understand how and why the bisection method works. Know the fixed point ite ...
Calculus Scholarship Achievement Standard
... Problems may include unfamiliar situations which: are those which students would not be expected to have practised in normal classwork require innovative thinking. ...
... Problems may include unfamiliar situations which: are those which students would not be expected to have practised in normal classwork require innovative thinking. ...
Unlicensed-7-PDF801-804_engineering optimization
... [B.4]. Sargent and Sebastian presented numerical experiences with unconstrained minimization algorithms [B.5]. On the basis of these studies, the following general conclusions can be drawn. If the first and second derivatives of the objective function ( f ) can be evaluated easily (either in closed ...
... [B.4]. Sargent and Sebastian presented numerical experiences with unconstrained minimization algorithms [B.5]. On the basis of these studies, the following general conclusions can be drawn. If the first and second derivatives of the objective function ( f ) can be evaluated easily (either in closed ...
Editorial This special issue is devoted to Numerical Modelling in
... performance computers and parallel computations have been introduced in all scientific branches. The number of applications of parallel computations, as well as attention devoted to the parallel computers, their programming and parallel algorithms have been increasing tremendously making significant ...
... performance computers and parallel computations have been introduced in all scientific branches. The number of applications of parallel computations, as well as attention devoted to the parallel computers, their programming and parallel algorithms have been increasing tremendously making significant ...
Circuit Improvements for the TL-922
... Fix for problem 1: Install a stepstart circuit for the entire amplifier. All that's needed is a 100vdc, or 12vdc, or 24vdc-coil; dpdt relay with 10A contacts, and a pair of 25 Ohm, 7 - 10 watt resistors. If a 12v or 24v coil relay is used, a rectifier-capacitor filter circuit is added to rectify the ...
... Fix for problem 1: Install a stepstart circuit for the entire amplifier. All that's needed is a 100vdc, or 12vdc, or 24vdc-coil; dpdt relay with 10A contacts, and a pair of 25 Ohm, 7 - 10 watt resistors. If a 12v or 24v coil relay is used, a rectifier-capacitor filter circuit is added to rectify the ...
Chapter 12: Copying with the Limitations of Algorithm Power
... Tackling Difficult Combinatorial Problems There are two principal approaches to tackling difficult combinatorial problems (NP-hard problems): ...
... Tackling Difficult Combinatorial Problems There are two principal approaches to tackling difficult combinatorial problems (NP-hard problems): ...
Finding Complex Solutions of Polynomial Equations
... through zero at t 1, 2, and 7 seconds. Write the simplest polynomial describing the voltage V(t). ...
... through zero at t 1, 2, and 7 seconds. Write the simplest polynomial describing the voltage V(t). ...
Physics 517/617 HOMEWORK IV Due: Nov 10
... 4) Simpson, problem 10, page 252. In this problem assume that the emitter is grounded and the collector resistor is connected between the collector and power supply (e.g. Fig. 5.8). 5) Simpson, problem 11, page 252. Physics 617 or optional 1) Use the B2SPICE program on the computers in Room 3005 to ...
... 4) Simpson, problem 10, page 252. In this problem assume that the emitter is grounded and the collector resistor is connected between the collector and power supply (e.g. Fig. 5.8). 5) Simpson, problem 11, page 252. Physics 617 or optional 1) Use the B2SPICE program on the computers in Room 3005 to ...
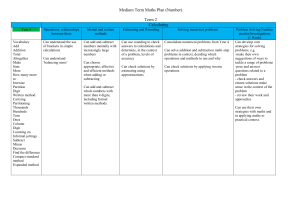
Term 2
... Can using the relations of perimeter or area to find unknown lengths. Can measure and calculate the perimeter of composite rectilinear shapes in centimetres and metres Can calculate and compare the area of rectangles (including squares), including using standard units, square centimetres (cm²) and s ...
... Can using the relations of perimeter or area to find unknown lengths. Can measure and calculate the perimeter of composite rectilinear shapes in centimetres and metres Can calculate and compare the area of rectangles (including squares), including using standard units, square centimetres (cm²) and s ...
Physics 517/617 HOMEWORK IV Due: July 25
... 2) Simpson, problem 27, page 198. 3) Simpson, problem 6, page 252. 4) Simpson, problem 10, page 252. In this problem assume that the emitter is grounded and the collector resistor is connected between the collector and power supply (e.g. Fig. 5.8). 5) Simpson, problem 11, page 252. Physics 617 or op ...
... 2) Simpson, problem 27, page 198. 3) Simpson, problem 6, page 252. 4) Simpson, problem 10, page 252. In this problem assume that the emitter is grounded and the collector resistor is connected between the collector and power supply (e.g. Fig. 5.8). 5) Simpson, problem 11, page 252. Physics 617 or op ...
Physics 517/617 HOMEWORK IV Due: July 26
... 2) Simpson, problem 27, page 198. 3) Simpson, problem 6, page 252. 4) Simpson, problem 10, page 252. In this problem assume that the emitter is grounded and the collector resistor is connected between the collector and power supply (e.g. Fig. 5.8). 5) Simpson, problem 11, page 252. Physics 617 or op ...
... 2) Simpson, problem 27, page 198. 3) Simpson, problem 6, page 252. 4) Simpson, problem 10, page 252. In this problem assume that the emitter is grounded and the collector resistor is connected between the collector and power supply (e.g. Fig. 5.8). 5) Simpson, problem 11, page 252. Physics 617 or op ...
Physics 4700 HOMEWORK IV Due: Oct 19
... 2) Simpson, problem 27, page 198. 3) Simpson, problem 6, page 252. 4) Simpson, problem 10, page 252. In this problem assume that the emitter is grounded and the collector resistor is connected between the collector and power supply (e.g. Fig. 5.8). 5) Simpson, problem 11, page 252. 6) Use the 5SPICE ...
... 2) Simpson, problem 27, page 198. 3) Simpson, problem 6, page 252. 4) Simpson, problem 10, page 252. In this problem assume that the emitter is grounded and the collector resistor is connected between the collector and power supply (e.g. Fig. 5.8). 5) Simpson, problem 11, page 252. 6) Use the 5SPICE ...
Physics 4700 HOMEWORK IV Due: March 9
... 2) Simpson, problem 27, page 198. 3) Simpson, problem 6, page 252. 4) Simpson, problem 10, page 252. In this problem assume that the emitter is grounded and the collector resistor is connected between the collector and power supply (e.g. Fig. 5.8). 5) Simpson, problem 11, page 252. 6) Use the 5SPICE ...
... 2) Simpson, problem 27, page 198. 3) Simpson, problem 6, page 252. 4) Simpson, problem 10, page 252. In this problem assume that the emitter is grounded and the collector resistor is connected between the collector and power supply (e.g. Fig. 5.8). 5) Simpson, problem 11, page 252. 6) Use the 5SPICE ...
Here
... 5. Develop the elements equations for a 10-cm rod with boundary conditions of T(0, t) = 40 and T(10, t) = 100 and a uniform heat source of f(x) = 20. Employ four equal-size elements of length = 2.5 cm. Compute the temperature distribution for the entire rod. dc d 2c 6 Use Galerkin’s method to develo ...
... 5. Develop the elements equations for a 10-cm rod with boundary conditions of T(0, t) = 40 and T(10, t) = 100 and a uniform heat source of f(x) = 20. Employ four equal-size elements of length = 2.5 cm. Compute the temperature distribution for the entire rod. dc d 2c 6 Use Galerkin’s method to develo ...
Instructions Example 1. Carefully read the problem, note what
... numerical data is given, and what is being asked for. 2. Make a sketch, drawing, or picture of the described situation, and put all the given data from the problem on the drawing. Look for what the problem’s question is. In other words, what do they want to know? In this example, they want to know w ...
... numerical data is given, and what is being asked for. 2. Make a sketch, drawing, or picture of the described situation, and put all the given data from the problem on the drawing. Look for what the problem’s question is. In other words, what do they want to know? In this example, they want to know w ...
Physics 517/617 HOMEWORK VII Due August 22
... 1) Simpson: problem 3, page 595. 2) Convert the following binary numbers to decimal: a) 1110101.0110 b) 11.01010101...repeats 3) Simpson: problem 10, page 595. 4) Simpson: problem 12, page 596. Note: there is a typo in the circuit drawing for this problem. The D2 near D1 should read D0 . 5) Simpson: ...
... 1) Simpson: problem 3, page 595. 2) Convert the following binary numbers to decimal: a) 1110101.0110 b) 11.01010101...repeats 3) Simpson: problem 10, page 595. 4) Simpson: problem 12, page 596. Note: there is a typo in the circuit drawing for this problem. The D2 near D1 should read D0 . 5) Simpson: ...
Physics 517/617 HOMEWORK VII Due August 24
... 1) Simpson: problem 3, page 595. 2) Convert the following binary numbers to decimal: a) 1110101.0110 b) 11.01010101...repeats 3) Simpson: problem 10, page 595. 4) Simpson: problem 12, page 596. Note: there is a typo in the circuit drawing for this problem. The D2 near D1 should read D0 . 5) Simpson: ...
... 1) Simpson: problem 3, page 595. 2) Convert the following binary numbers to decimal: a) 1110101.0110 b) 11.01010101...repeats 3) Simpson: problem 10, page 595. 4) Simpson: problem 12, page 596. Note: there is a typo in the circuit drawing for this problem. The D2 near D1 should read D0 . 5) Simpson: ...
Physics 4700 HOMEWORK VII Due April 13
... 1) Simpson: problem 3, page 595. 2) Convert the following binary numbers to decimal: a) 1110101.0110 b) 11.01010101...repeats 3) Simpson: problem 10, page 595. 4) Simpson: problem 12, page 596. Note: there is a typo in the circuit drawing for this problem. The D2 near D1 should read D0. 5) Simpson: ...
... 1) Simpson: problem 3, page 595. 2) Convert the following binary numbers to decimal: a) 1110101.0110 b) 11.01010101...repeats 3) Simpson: problem 10, page 595. 4) Simpson: problem 12, page 596. Note: there is a typo in the circuit drawing for this problem. The D2 near D1 should read D0. 5) Simpson: ...
Physics 4700 HOMEWORK VII Due Nov 30
... 1) Simpson: problem 3, page 595. 2) Convert the following binary numbers to decimal: a) 1110101.0110 b) 11.01010101...repeats 3) Simpson: problem 10, page 595. 4) Simpson: problem 12, page 596. Note: there is a typo in the circuit drawing for this problem. The D2 near D1 should read D0. 5) Simpson: ...
... 1) Simpson: problem 3, page 595. 2) Convert the following binary numbers to decimal: a) 1110101.0110 b) 11.01010101...repeats 3) Simpson: problem 10, page 595. 4) Simpson: problem 12, page 596. Note: there is a typo in the circuit drawing for this problem. The D2 near D1 should read D0. 5) Simpson: ...
P versus NP problem
The P versus NP problem is a major unsolved problem in computer science. Informally, it asks whether every problem whose solution can be quickly verified by a computer can also be quickly solved by a computer. It was essentially first mentioned in a 1956 letter written by Kurt Gödel to John von Neumann. Gödel asked whether a certain NP-complete problem could be solved in quadratic or linear time. The precise statement of the P versus NP problem was introduced in 1971 by Stephen Cook in his seminal paper ""The complexity of theorem proving procedures"" and is considered by many to be the most important open problem in the field. It is one of the seven Millennium Prize Problems selected by the Clay Mathematics Institute to carry a US$1,000,000 prize for the first correct solution.The informal term quickly, used above, means the existence of an algorithm for the task that runs in polynomial time. The general class of questions for which some algorithm can provide an answer in polynomial time is called ""class P"" or just ""P"". For some questions, there is no known way to find an answer quickly, but if one is provided with information showing what the answer is, it is possible to verify the answer quickly. The class of questions for which an answer can be verified in polynomial time is called NP.Consider the subset sum problem, an example of a problem that is easy to verify, but whose answer may be difficult to compute. Given a set of integers, does some nonempty subset of them sum to 0? For instance, does a subset of the set {−2, −3, 15, 14, 7, −10} add up to 0? The answer ""yes, because the subset {−2, −3, −10, 15} adds up to zero"" can be quickly verified with three additions. However, there is no known algorithm to find such a subset in polynomial time (there is one, however, in exponential time, which consists of 2n-n-1 tries), but such an algorithm exists if P = NP; hence this problem is in NP (quickly checkable) but not necessarily in P (quickly solvable).An answer to the P = NP question would determine whether problems that can be verified in polynomial time, like the subset-sum problem, can also be solved in polynomial time. If it turned out that P ≠ NP, it would mean that there are problems in NP (such as NP-complete problems) that are harder to compute than to verify: they could not be solved in polynomial time, but the answer could be verified in polynomial time.Aside from being an important problem in computational theory, a proof either way would have profound implications for mathematics, cryptography, algorithm research, artificial intelligence, game theory, multimedia processing, philosophy, economics and many other fields.