Birkeland, Darboux and Poincaré: Motion of an Electric Charge in
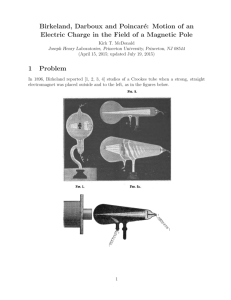
... this line, colliding with the magnetic pole. In this case the minimum distance of approach of the charge to the pole is x0 = 0. It turns out that for extremely small but nonzero x0 a charged particle with spin (such as an electron or proton) also collides with the pole in a classical analysis, as di ...
... this line, colliding with the magnetic pole. In this case the minimum distance of approach of the charge to the pole is x0 = 0. It turns out that for extremely small but nonzero x0 a charged particle with spin (such as an electron or proton) also collides with the pole in a classical analysis, as di ...
How to Determine the Probability of the Higgs Boson Detection
... Public interest. The amount of research funds spent for the Higgs detection is extraordinary. A Superconducting Super Collider project was cancelled in 1993 in the US, but also the three billion dollar LHC construction has raised criticism on high energy physics receiving unproportional funding. Th ...
... Public interest. The amount of research funds spent for the Higgs detection is extraordinary. A Superconducting Super Collider project was cancelled in 1993 in the US, but also the three billion dollar LHC construction has raised criticism on high energy physics receiving unproportional funding. Th ...
CHAPTER 2 FLOW PAST A SPHERE I: DIMENSIONAL ANALYSIS
... 10 Equation 2.2 is an equivalent but dimensionless form of Equation 2.1. The great advantage of the dimensionless equation is that it involves only two variables—a dependent dimensionless variable FD/ρU2D2 and an independent dimensionless variable ρUD/μ—instead of the original five. Think of the eno ...
... 10 Equation 2.2 is an equivalent but dimensionless form of Equation 2.1. The great advantage of the dimensionless equation is that it involves only two variables—a dependent dimensionless variable FD/ρU2D2 and an independent dimensionless variable ρUD/μ—instead of the original five. Think of the eno ...
Thesis - Institut für Physik
... Their dynamics can be described by the many-body Schrödinger equation, but analytic solutions are rare exceptions and approximations and numerical methods are generally indispensable. For weakly interacting systems, a mean field theory like the Gross-Pitaevskii equation gives a good approximation. I ...
... Their dynamics can be described by the many-body Schrödinger equation, but analytic solutions are rare exceptions and approximations and numerical methods are generally indispensable. For weakly interacting systems, a mean field theory like the Gross-Pitaevskii equation gives a good approximation. I ...
phys1443-fall04-111504
... Example for Rigid Body Angular Momentum A rigid rod of mass M and length l is pivoted without friction at its center. Two particles of mass m1 and m2 are attached to either end of the rod. The combination rotates on a vertical plane with an angular speed of . Find an expression for the magnitude o ...
... Example for Rigid Body Angular Momentum A rigid rod of mass M and length l is pivoted without friction at its center. Two particles of mass m1 and m2 are attached to either end of the rod. The combination rotates on a vertical plane with an angular speed of . Find an expression for the magnitude o ...
2012) all (F I
... 9 Oct Schrödinger’s wave equation and interpreting the wave function Wed 10 Oct Quiz 7; Classical connections: Ehrenfest’s Theorem; the Hamilton-Jacobi Equation Thu 11 Oct Solving the simple harmonic oscillator with Schrödinger’s Equation and generating functions ...
... 9 Oct Schrödinger’s wave equation and interpreting the wave function Wed 10 Oct Quiz 7; Classical connections: Ehrenfest’s Theorem; the Hamilton-Jacobi Equation Thu 11 Oct Solving the simple harmonic oscillator with Schrödinger’s Equation and generating functions ...
physics 220 - Purdue Physics
... – The magnitude of the velocity is called the speed – This is the distance traveled per unit of time – Depends on the length of the actual path between the initial and final positions ...
... – The magnitude of the velocity is called the speed – This is the distance traveled per unit of time – Depends on the length of the actual path between the initial and final positions ...
QUANTUM MONTE CARLO SIMULATION OF TUNNELLING DEVICES USING WAVEPACKETS AND BOHM TRAJECTORIES
... I have read somewhere that science has to be considered as a type of culture at the same level as painting, playing music or writing poetry. It indicates the human development of the society. However, science is also an economical motor of our society because its has a direct impact on our everyday ...
... I have read somewhere that science has to be considered as a type of culture at the same level as painting, playing music or writing poetry. It indicates the human development of the society. However, science is also an economical motor of our society because its has a direct impact on our everyday ...
Cavity dark states for quantum computing M.S. Shahriar , J.A. Bowers
... eective rate of decoherence due to cavity photon decay is thus reduced by nearly three orders of magnitude. Thus, the cavity dark state described here achieves the desired transfer of quantum information without being aected signi®cantly by the cavity decay, and yet does not take much longer than ...
... eective rate of decoherence due to cavity photon decay is thus reduced by nearly three orders of magnitude. Thus, the cavity dark state described here achieves the desired transfer of quantum information without being aected signi®cantly by the cavity decay, and yet does not take much longer than ...
Notes on Semiclassical Gravity
... the energy-momentum tensor can act as the source for a semiclassical, c-number, gravitational field. The basic issues can be understood from the study of the semiclassical limit of a toy model, consisting of two interacting particles, which mimics the essential properties of quantum general relativi ...
... the energy-momentum tensor can act as the source for a semiclassical, c-number, gravitational field. The basic issues can be understood from the study of the semiclassical limit of a toy model, consisting of two interacting particles, which mimics the essential properties of quantum general relativi ...
Undergraduate Quantum Chemistry Written by Jussi Eloranta
... by E = hν. Albert Einstein suggested that photons have relativistic mass m given by E = mc2 . Combining these equations gives (p = momentum, ν = frequency, λ = wavelength and c = νλ): ...
... by E = hν. Albert Einstein suggested that photons have relativistic mass m given by E = mc2 . Combining these equations gives (p = momentum, ν = frequency, λ = wavelength and c = νλ): ...
Quantum Monte Carlo study of the Ne atom and the Ne+ ion
... Optimizing the orbitals reduces the VMC energy, but does not have a significant effect on the DMC energy, except in the case of the pseudopotential calculation with backflow correlations, where optimizing the orbitals actually increases the DMC energy, presumably because the very large number of var ...
... Optimizing the orbitals reduces the VMC energy, but does not have a significant effect on the DMC energy, except in the case of the pseudopotential calculation with backflow correlations, where optimizing the orbitals actually increases the DMC energy, presumably because the very large number of var ...
For each pair of similar figures, find the area of the green figure. 1
... initial volume using the STAT PLOT feature on your feature to approximate the function represented by th d. ALGEBRAIC Write an algebraic expression for in terms of scale factor k. SOLUTION: a. For the table, each dimension (length, width, or hei volume will be the product of all the dimensions. ...
... initial volume using the STAT PLOT feature on your feature to approximate the function represented by th d. ALGEBRAIC Write an algebraic expression for in terms of scale factor k. SOLUTION: a. For the table, each dimension (length, width, or hei volume will be the product of all the dimensions. ...
Direct Observation of Second Order Atom
... smaller than the tunnel matrix element J (J/U~1.5, Fig. 2a and b), tunnelling of a single atom out of a pair is only slightly detuned. This process therefore competes with the resonant second order tunnel process, leading to a signal containing more than one frequency component (see Fig. 2b). When r ...
... smaller than the tunnel matrix element J (J/U~1.5, Fig. 2a and b), tunnelling of a single atom out of a pair is only slightly detuned. This process therefore competes with the resonant second order tunnel process, leading to a signal containing more than one frequency component (see Fig. 2b). When r ...
Full text in PDF form
... There are three main approaches to quantum gravity: the canonical approach, the histories approach, and string theory. In what follows, we will focus mainly on the canonical approach; however, we will consider also quantum histories in the context of topos theory [1-2]. A novel interest in the canon ...
... There are three main approaches to quantum gravity: the canonical approach, the histories approach, and string theory. In what follows, we will focus mainly on the canonical approach; however, we will consider also quantum histories in the context of topos theory [1-2]. A novel interest in the canon ...
Renormalization group

In theoretical physics, the renormalization group (RG) refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales. In particle physics, it reflects the changes in the underlying force laws (codified in a quantum field theory) as the energy scale at which physical processes occur varies, energy/momentum and resolution distance scales being effectively conjugate under the uncertainty principle (cf. Compton wavelength).A change in scale is called a ""scale transformation"". The renormalization group is intimately related to ""scale invariance"" and ""conformal invariance"", symmetries in which a system appears the same at all scales (so-called self-similarity). (However, note that scale transformations are included in conformal transformations, in general: the latter including additional symmetry generators associated with special conformal transformations.)As the scale varies, it is as if one is changing the magnifying power of a notional microscope viewing the system. In so-called renormalizable theories, the system at one scale will generally be seen to consist of self-similar copies of itself when viewed at a smaller scale, with different parameters describing the components of the system. The components, or fundamental variables, may relate to atoms, elementary particles, atomic spins, etc. The parameters of the theory typically describe the interactions of the components. These may be variable ""couplings"" which measure the strength of various forces, or mass parameters themselves. The components themselves may appear to be composed of more of the self-same components as one goes to shorter distances.For example, in quantum electrodynamics (QED), an electron appears to be composed of electrons, positrons (anti-electrons) and photons, as one views it at higher resolution, at very short distances. The electron at such short distances has a slightly different electric charge than does the ""dressed electron"" seen at large distances, and this change, or ""running,"" in the value of the electric charge is determined by the renormalization group equation.