The Homological Nature of Entropy
... where SI denotes the join of the Si such that i ∈ I. We have I1 = H and I2 = I is the usual mutual information: I(S; T ) = H(S) + H(T ) − H(S, T ) . Theorem B. (cf. section 3, [7]): I2m = δt δδt ...δδt H, I2m+1 = −δδt δδt ...δδt H, where there are m − 1 δ and m δt factors for I2m and m δ and m δt fa ...
... where SI denotes the join of the Si such that i ∈ I. We have I1 = H and I2 = I is the usual mutual information: I(S; T ) = H(S) + H(T ) − H(S, T ) . Theorem B. (cf. section 3, [7]): I2m = δt δδt ...δδt H, I2m+1 = −δδt δδt ...δδt H, where there are m − 1 δ and m δt factors for I2m and m δ and m δt fa ...
Calculation of Van der Waals interaction strength between rubidium
... interference. For the Rydberg state 100s we see that there is a resonant dipole-dipole interaction which scales as 1/R3 at small interatomic distances and a van der Waals interaction, which scales as 1/R6 at large interatomic distances. The cross-over distance Rc will depend on the principal quantum ...
... interference. For the Rydberg state 100s we see that there is a resonant dipole-dipole interaction which scales as 1/R3 at small interatomic distances and a van der Waals interaction, which scales as 1/R6 at large interatomic distances. The cross-over distance Rc will depend on the principal quantum ...
Document
... convergence and related topics will not be gone into until the need arises. It is desirable to have a special name for describing the vectors which are connected with the states of a system in quantum mechanics, whether they are in a space of a finite or an infinite number of dimensions. We shall ca ...
... convergence and related topics will not be gone into until the need arises. It is desirable to have a special name for describing the vectors which are connected with the states of a system in quantum mechanics, whether they are in a space of a finite or an infinite number of dimensions. We shall ca ...
Mathematics via Symmetry - Philsci
... unites the many different types of symmetries under what he calls “point of view invariance” (POVI). That is, all the laws of physics must be symmetric with respect to POVI. The laws must remain the same regardless of how they are viewed. Stenger ([Ste06]) demonstrates how much of modern physics can ...
... unites the many different types of symmetries under what he calls “point of view invariance” (POVI). That is, all the laws of physics must be symmetric with respect to POVI. The laws must remain the same regardless of how they are viewed. Stenger ([Ste06]) demonstrates how much of modern physics can ...
Report of PAC for Particle Physics
... boson decay rates into WW- or ZZ-pair at MHIGGS = 400 -- 1000 GeV. ...
... boson decay rates into WW- or ZZ-pair at MHIGGS = 400 -- 1000 GeV. ...
Quantum Information Processing through Nuclear Magnetic
... States like (1) are pure entangled, and like (2) are separable. In the language of density matrices, strongly separable states are those ones which can be written as ρ = ρA ⊗ ρB , and weakly separable those ones for which ρ = ∑i pi ρA,i ⊗ ρB,i where pi are probabilities for the occurrence of the pro ...
... States like (1) are pure entangled, and like (2) are separable. In the language of density matrices, strongly separable states are those ones which can be written as ρ = ρA ⊗ ρB , and weakly separable those ones for which ρ = ∑i pi ρA,i ⊗ ρB,i where pi are probabilities for the occurrence of the pro ...
Electronic Structure of Clusters and Nanocrystals
... volume. Other extensive properties include thermodynamics properties like the heat capacity, enthalpy, entropy and free energy of the system. Matter at the nanoscale is different. Properties that are intensive at the macroscopic scale may not be intensive at the “nano-” or “subnano-” scale. In fact, ...
... volume. Other extensive properties include thermodynamics properties like the heat capacity, enthalpy, entropy and free energy of the system. Matter at the nanoscale is different. Properties that are intensive at the macroscopic scale may not be intensive at the “nano-” or “subnano-” scale. In fact, ...
The origin of the phase in the interference of Bose
... local field that is used theoretically to choose a phase direction for a Bose condensate does not exist in nature. The treatment of phase 共actually relative phase兲 in Sec. IV, and the spontaneous appearance of a relative phase under the effect of the measurement of particle position in Fock states a ...
... local field that is used theoretically to choose a phase direction for a Bose condensate does not exist in nature. The treatment of phase 共actually relative phase兲 in Sec. IV, and the spontaneous appearance of a relative phase under the effect of the measurement of particle position in Fock states a ...
Quantum Probability and Decision Theory, Revisited
... (such as on which die-face is uppermost), although it need not be a formal wager: in the case of the road, for instance, one payoff scheme might refer to crossing the road, so that P(bus in road)=being hit by bus, P(no bus)=getting safely to other side; another might refer to choosing not to ...
... (such as on which die-face is uppermost), although it need not be a formal wager: in the case of the road, for instance, one payoff scheme might refer to crossing the road, so that P(bus in road)=being hit by bus, P(no bus)=getting safely to other side; another might refer to choosing not to ...
Quantization in singular real polarizations: K\" ahler regularization
... explicitly (see the no-go Theorem 3.4 and the Conjecture 3.5 below). Building up on previous works [BFMN, KW2, KMN1, MN1], in [MN2] a general strategy is proposed to find families of well behaved polarizations degenerating to a wide class of singular real polarizations corresponding to the level set ...
... explicitly (see the no-go Theorem 3.4 and the Conjecture 3.5 below). Building up on previous works [BFMN, KW2, KMN1, MN1], in [MN2] a general strategy is proposed to find families of well behaved polarizations degenerating to a wide class of singular real polarizations corresponding to the level set ...
Paper
... tween the two Fermi surfaces exceeds the energy gained from pairing – the so-called Chandrasekhar– Clogston (CC) limit of superconductivity. The issue of pairing and fermionic superfluidity in an imbalanced Fermi mixture has intrigued physicists for many decades. Although a population imbalance can ...
... tween the two Fermi surfaces exceeds the energy gained from pairing – the so-called Chandrasekhar– Clogston (CC) limit of superconductivity. The issue of pairing and fermionic superfluidity in an imbalanced Fermi mixture has intrigued physicists for many decades. Although a population imbalance can ...
Perfect state transfer over distance
... computers good communication between different parts of the system is essential. The need is thus to transfer quantum states and generate entanglement between different regions contained within the system. There are various physical systems that can serve as quantum channels, one of them being a qua ...
... computers good communication between different parts of the system is essential. The need is thus to transfer quantum states and generate entanglement between different regions contained within the system. There are various physical systems that can serve as quantum channels, one of them being a qua ...
Statistical Properties of the Squeezed Displaced Number States
... Squeezed Displaced Number States of the light were introduced in the recent literature. They exhibit various nonclassical properties as sub-Poissonian statistics, squeezing and oscillations in the photon-number distribution. Here we investigate other properties of these elds, as waiting-time and ph ...
... Squeezed Displaced Number States of the light were introduced in the recent literature. They exhibit various nonclassical properties as sub-Poissonian statistics, squeezing and oscillations in the photon-number distribution. Here we investigate other properties of these elds, as waiting-time and ph ...
Slip Sliding Along
... Answer: While we have considered several examples in which the total momentum of the system is zero, this is not the most general case. The momentum of a system can have any magnitude and any direction before the collision. If momentum is conserved, the momentum of the system always has the same mag ...
... Answer: While we have considered several examples in which the total momentum of the system is zero, this is not the most general case. The momentum of a system can have any magnitude and any direction before the collision. If momentum is conserved, the momentum of the system always has the same mag ...
Quantum Theory: a Pragmatist Approach
... account of probability! Of course, he would insist that different persons may, and often do, hold different beliefs, which makes probability personalist—varying from person to person—and to that extent subjective. On other “subjectivist” views, an agent’s degrees of belief count as probabilities onl ...
... account of probability! Of course, he would insist that different persons may, and often do, hold different beliefs, which makes probability personalist—varying from person to person—and to that extent subjective. On other “subjectivist” views, an agent’s degrees of belief count as probabilities onl ...
Birkeland, Darboux and Poincaré: Motion of an Electric Charge in
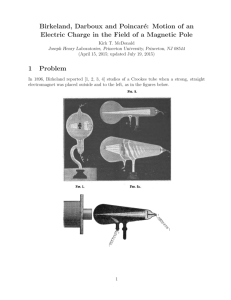
... this line, colliding with the magnetic pole. In this case the minimum distance of approach of the charge to the pole is x0 = 0. It turns out that for extremely small but nonzero x0 a charged particle with spin (such as an electron or proton) also collides with the pole in a classical analysis, as di ...
... this line, colliding with the magnetic pole. In this case the minimum distance of approach of the charge to the pole is x0 = 0. It turns out that for extremely small but nonzero x0 a charged particle with spin (such as an electron or proton) also collides with the pole in a classical analysis, as di ...
Renormalization group

In theoretical physics, the renormalization group (RG) refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales. In particle physics, it reflects the changes in the underlying force laws (codified in a quantum field theory) as the energy scale at which physical processes occur varies, energy/momentum and resolution distance scales being effectively conjugate under the uncertainty principle (cf. Compton wavelength).A change in scale is called a ""scale transformation"". The renormalization group is intimately related to ""scale invariance"" and ""conformal invariance"", symmetries in which a system appears the same at all scales (so-called self-similarity). (However, note that scale transformations are included in conformal transformations, in general: the latter including additional symmetry generators associated with special conformal transformations.)As the scale varies, it is as if one is changing the magnifying power of a notional microscope viewing the system. In so-called renormalizable theories, the system at one scale will generally be seen to consist of self-similar copies of itself when viewed at a smaller scale, with different parameters describing the components of the system. The components, or fundamental variables, may relate to atoms, elementary particles, atomic spins, etc. The parameters of the theory typically describe the interactions of the components. These may be variable ""couplings"" which measure the strength of various forces, or mass parameters themselves. The components themselves may appear to be composed of more of the self-same components as one goes to shorter distances.For example, in quantum electrodynamics (QED), an electron appears to be composed of electrons, positrons (anti-electrons) and photons, as one views it at higher resolution, at very short distances. The electron at such short distances has a slightly different electric charge than does the ""dressed electron"" seen at large distances, and this change, or ""running,"" in the value of the electric charge is determined by the renormalization group equation.