Chapter 3
... The subject then happened to arise in conversation between Schrodinger and Debye. Both professed not to have understood the work. Result: Debye proposed that Schrödinger should give a colloquium about it! This he did in November or December 1925 as one of their current joint E.T.H.-University series ...
... The subject then happened to arise in conversation between Schrodinger and Debye. Both professed not to have understood the work. Result: Debye proposed that Schrödinger should give a colloquium about it! This he did in November or December 1925 as one of their current joint E.T.H.-University series ...
The Elegant Universe: Part 2
... NARRATOR: Obsession drives scientists to pursue the Holy Grail of physics, but are they ready for what they discover? Step into the bizarre world of the Elegant Universe right now. BRIAN GREENE: It's a little known secret but for more than half a century a dark cloud has been looming over modern sci ...
... NARRATOR: Obsession drives scientists to pursue the Holy Grail of physics, but are they ready for what they discover? Step into the bizarre world of the Elegant Universe right now. BRIAN GREENE: It's a little known secret but for more than half a century a dark cloud has been looming over modern sci ...
File
... energy when they are in a stable orbit, but his model offered no explanation for this. – Another problem with Bohr’s model was that it could not explain why electrons always have certain stable orbits • For these reasons, scientists continued to search for a new model of the atom. Chapter menu ...
... energy when they are in a stable orbit, but his model offered no explanation for this. – Another problem with Bohr’s model was that it could not explain why electrons always have certain stable orbits • For these reasons, scientists continued to search for a new model of the atom. Chapter menu ...
chapter 7 blm answer key
... John Wallis was one of the founders of the Royal Society. He was also one of the first scientists to suggest the law of the conservation of momentum when, in 1668, the Royal Society accepted the challenge to investigate the behaviour of colliding bodies. Wallis is credited with the discovery of the ...
... John Wallis was one of the founders of the Royal Society. He was also one of the first scientists to suggest the law of the conservation of momentum when, in 1668, the Royal Society accepted the challenge to investigate the behaviour of colliding bodies. Wallis is credited with the discovery of the ...
Physics 235 Chapter 09 Chapter 9
... In this Chapter we expand our discussion from the two-body systems discussed in Chapter 8 to systems that consist out of many particles. In general, these particles are exposed to both external and internal forces. In our discussion in the Chapter we will make the following assumptions about the int ...
... In this Chapter we expand our discussion from the two-body systems discussed in Chapter 8 to systems that consist out of many particles. In general, these particles are exposed to both external and internal forces. In our discussion in the Chapter we will make the following assumptions about the int ...
Phys. Rev. Lett. 115, 155302
... where n is the density and a > 0 and g ¼ 4πℏ2 a=m are, respectively, the scattering length and coupling constant characterizing the interparticle interaction. The LHY correction originates from the zero-point motion of the Bogoliubov excitations and is thus intrinsically quantum. It is also universa ...
... where n is the density and a > 0 and g ¼ 4πℏ2 a=m are, respectively, the scattering length and coupling constant characterizing the interparticle interaction. The LHY correction originates from the zero-point motion of the Bogoliubov excitations and is thus intrinsically quantum. It is also universa ...
CHAPTER 18: ELECTRIC CHARGE AND ELECTRIC FIELD
... Next we need to determine the number of electrons we removed to leave a net charge of 2.00 µC . We need to remove − 2.00 µC of charge, so the number of electrons to be removed is given by ...
... Next we need to determine the number of electrons we removed to leave a net charge of 2.00 µC . We need to remove − 2.00 µC of charge, so the number of electrons to be removed is given by ...
Finite Element Method for Finite-Size Scaling in Quantum Mechanics
... energy. These singularities occur only in the thermodynamic limit1,2 where the dimension of the system approaches infinity. However, calculations are done only on finite systems. A finitesize scaling (FSS) approach is needed in order to exptrapolate results from finite systems to the thermodynamic l ...
... energy. These singularities occur only in the thermodynamic limit1,2 where the dimension of the system approaches infinity. However, calculations are done only on finite systems. A finitesize scaling (FSS) approach is needed in order to exptrapolate results from finite systems to the thermodynamic l ...
Gender Studies and High Energy Physics
... The absence of women in neutrino physics Proceedings of the 2nd ICESHS, 2006 While I was working on the history of the discipline of neutrino physics I was shocked by the absence of women in all the brief histories related to the discipline. The first question arose: Are there any women in the field ...
... The absence of women in neutrino physics Proceedings of the 2nd ICESHS, 2006 While I was working on the history of the discipline of neutrino physics I was shocked by the absence of women in all the brief histories related to the discipline. The first question arose: Are there any women in the field ...
Transition Probability (Fidelity) and its Relatives
... [13] is a general reference to the geometric phase for general states. For relations to Einstein-Yang-Mills systems see [28]. For comparison with other approach see [27]. A treatment of the dim H = ∞ case is in [14]. Other aspects, including the problem of experimental verifications are in [2] and i ...
... [13] is a general reference to the geometric phase for general states. For relations to Einstein-Yang-Mills systems see [28]. For comparison with other approach see [27]. A treatment of the dim H = ∞ case is in [14]. Other aspects, including the problem of experimental verifications are in [2] and i ...
1 Press release Brussels, 8 October 2013 Nobel Prize for
... University, the person responsible for introducing spontaneous symmetry breaking into elementary particle theory and who went on to receive the Nobel Prize for Physics in 2008. This put us on to studying the elementary particle theory. At that time, long-range forces (i.e. forces acting on far dista ...
... University, the person responsible for introducing spontaneous symmetry breaking into elementary particle theory and who went on to receive the Nobel Prize for Physics in 2008. This put us on to studying the elementary particle theory. At that time, long-range forces (i.e. forces acting on far dista ...
Use Similar Polygons (6
... Definition: If two polygons are similar, the Scale Factor is the ratio of the lengths of any two corresponding sides. Ex. Find the scale factor of the similar polygons below ...
... Definition: If two polygons are similar, the Scale Factor is the ratio of the lengths of any two corresponding sides. Ex. Find the scale factor of the similar polygons below ...
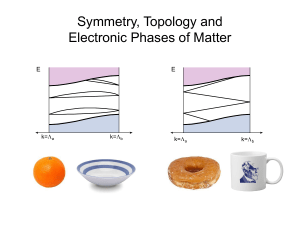
Renormalization group

In theoretical physics, the renormalization group (RG) refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales. In particle physics, it reflects the changes in the underlying force laws (codified in a quantum field theory) as the energy scale at which physical processes occur varies, energy/momentum and resolution distance scales being effectively conjugate under the uncertainty principle (cf. Compton wavelength).A change in scale is called a ""scale transformation"". The renormalization group is intimately related to ""scale invariance"" and ""conformal invariance"", symmetries in which a system appears the same at all scales (so-called self-similarity). (However, note that scale transformations are included in conformal transformations, in general: the latter including additional symmetry generators associated with special conformal transformations.)As the scale varies, it is as if one is changing the magnifying power of a notional microscope viewing the system. In so-called renormalizable theories, the system at one scale will generally be seen to consist of self-similar copies of itself when viewed at a smaller scale, with different parameters describing the components of the system. The components, or fundamental variables, may relate to atoms, elementary particles, atomic spins, etc. The parameters of the theory typically describe the interactions of the components. These may be variable ""couplings"" which measure the strength of various forces, or mass parameters themselves. The components themselves may appear to be composed of more of the self-same components as one goes to shorter distances.For example, in quantum electrodynamics (QED), an electron appears to be composed of electrons, positrons (anti-electrons) and photons, as one views it at higher resolution, at very short distances. The electron at such short distances has a slightly different electric charge than does the ""dressed electron"" seen at large distances, and this change, or ""running,"" in the value of the electric charge is determined by the renormalization group equation.