Why Quantum Computing? - Quantum Physics and Quantum
... or f 1with probability ½. These are classically mutually exclusive. * Quantum mechanically these two alternatives can INTERFERE to yield some global property of the function f and by using a Hadamard gate can recombine the different alternatives ...
... or f 1with probability ½. These are classically mutually exclusive. * Quantum mechanically these two alternatives can INTERFERE to yield some global property of the function f and by using a Hadamard gate can recombine the different alternatives ...
Nonperturbative quantum geometries
... infinite dimensional space of such solutions may be constructed. Physical states of quantum gravity must, in addition to being annihilated by the hamiltonian constraint, be invariant under the action of spatial diffeomorphisms. While most of the solutions to the hamiltonian constraint we have found ...
... infinite dimensional space of such solutions may be constructed. Physical states of quantum gravity must, in addition to being annihilated by the hamiltonian constraint, be invariant under the action of spatial diffeomorphisms. While most of the solutions to the hamiltonian constraint we have found ...
Early-stage relaxation of hot electrons by LO phonon emission Herve´ Castella
... 共SBE’s兲, which give the time evolution of the density distributions in both bands, and of the interband polarization.4 The scattering processes, however, are taken into account by instantaneous scattering rates as in Boltzmann equations, thus treating relaxation as totally incoherent and energy cons ...
... 共SBE’s兲, which give the time evolution of the density distributions in both bands, and of the interband polarization.4 The scattering processes, however, are taken into account by instantaneous scattering rates as in Boltzmann equations, thus treating relaxation as totally incoherent and energy cons ...
Chaos, Quantum-transactions and Consciousness
... The conscious mind can also be described functionally as an internal model of reality. While such an explanation does not address the basis of subjectivity, it does help explain some of the more bizarre states of consciousness and is supported by many actively constructive aspects of sensory process ...
... The conscious mind can also be described functionally as an internal model of reality. While such an explanation does not address the basis of subjectivity, it does help explain some of the more bizarre states of consciousness and is supported by many actively constructive aspects of sensory process ...
CHAPTER 2 Electron transfer in water and other polar environ
... envisaged in Marcus’ theory. There are two localized electronic states pictured. These are the two redox states. In one, a transferable electron is located at site A; in the other, the transferable charge is located on site B. If the state with the electron at site A is the initial state, species A− ...
... envisaged in Marcus’ theory. There are two localized electronic states pictured. These are the two redox states. In one, a transferable electron is located at site A; in the other, the transferable charge is located on site B. If the state with the electron at site A is the initial state, species A− ...
Nanowires for Quantum Optics - Leo Kouwenhoven
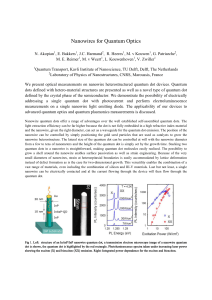
... advanced quantum optics and quantum plasmonics measurements is discussed. Nanowire quantum dots offer a range of advantages over the well established self-assembled quantum dots. The light extraction efficiency can be far higher because the dot is not fully embedded in a high refractive index materi ...
... advanced quantum optics and quantum plasmonics measurements is discussed. Nanowire quantum dots offer a range of advantages over the well established self-assembled quantum dots. The light extraction efficiency can be far higher because the dot is not fully embedded in a high refractive index materi ...
Few-Particle Effects in Semiconductor Quantum Dots: Spectrum Calculations on
... [5]. Together with effective mass approximation of semiconductor materials (section 2.1.1) and configuration interaction (CI) (chapter 2.2.2), so called few-carrier system can be solved in reasonable time frame without further approximation [6, 7]. Many works have devoted to the spectra prediction w ...
... [5]. Together with effective mass approximation of semiconductor materials (section 2.1.1) and configuration interaction (CI) (chapter 2.2.2), so called few-carrier system can be solved in reasonable time frame without further approximation [6, 7]. Many works have devoted to the spectra prediction w ...
Electron dephasing scattering rate in two
... whereas Fs共b兲 = 共1 / 2 + b兲 – ln共b兲. is the digamma function. The above expression for magnetoconductivity is valid for the diffusion approximation 共B Ⰶ Btr兲, where Btr = ប / 4eD is the transport field and D is the diffusion coefficient. The theory of the interaction is constructed for the ca ...
... whereas Fs共b兲 = 共1 / 2 + b兲 – ln共b兲. is the digamma function. The above expression for magnetoconductivity is valid for the diffusion approximation 共B Ⰶ Btr兲, where Btr = ប / 4eD is the transport field and D is the diffusion coefficient. The theory of the interaction is constructed for the ca ...
quantum - Word Format
... measurement with the wrong operator will perturb the state of the qubit. This means that when a qubit is measured, one must first choose the correct orientation and then apply the operator in order to get the true value. If the orientation of the polarization of each qubit is set at random, the long ...
... measurement with the wrong operator will perturb the state of the qubit. This means that when a qubit is measured, one must first choose the correct orientation and then apply the operator in order to get the true value. If the orientation of the polarization of each qubit is set at random, the long ...
Isolation of the Conceptual Ingredients of Quantum Theory by Toy
... not is contentious, but the paper spurred on other thinkers to show explicitly that a hidden variable interpretation of Quantum Theory would have to be ‘nonlocal’ [1, 13, 12].Einstein’s epithet for the notion of non-locality was “spukhafte fernwirkung” or “spooky action at a distance”, and he had pe ...
... not is contentious, but the paper spurred on other thinkers to show explicitly that a hidden variable interpretation of Quantum Theory would have to be ‘nonlocal’ [1, 13, 12].Einstein’s epithet for the notion of non-locality was “spukhafte fernwirkung” or “spooky action at a distance”, and he had pe ...
Scattering theory - Theory of Condensed Matter
... Almost everything we know about nuclei and elementary particles has been discovered in scattering experiments, from Rutherford’s surprise at finding that atoms have their mass and positive charge concentrated in almost pointlike nuclei, to the more recent discoveries, on a far smaller length scale, ...
... Almost everything we know about nuclei and elementary particles has been discovered in scattering experiments, from Rutherford’s surprise at finding that atoms have their mass and positive charge concentrated in almost pointlike nuclei, to the more recent discoveries, on a far smaller length scale, ...
Renormalization group

In theoretical physics, the renormalization group (RG) refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales. In particle physics, it reflects the changes in the underlying force laws (codified in a quantum field theory) as the energy scale at which physical processes occur varies, energy/momentum and resolution distance scales being effectively conjugate under the uncertainty principle (cf. Compton wavelength).A change in scale is called a ""scale transformation"". The renormalization group is intimately related to ""scale invariance"" and ""conformal invariance"", symmetries in which a system appears the same at all scales (so-called self-similarity). (However, note that scale transformations are included in conformal transformations, in general: the latter including additional symmetry generators associated with special conformal transformations.)As the scale varies, it is as if one is changing the magnifying power of a notional microscope viewing the system. In so-called renormalizable theories, the system at one scale will generally be seen to consist of self-similar copies of itself when viewed at a smaller scale, with different parameters describing the components of the system. The components, or fundamental variables, may relate to atoms, elementary particles, atomic spins, etc. The parameters of the theory typically describe the interactions of the components. These may be variable ""couplings"" which measure the strength of various forces, or mass parameters themselves. The components themselves may appear to be composed of more of the self-same components as one goes to shorter distances.For example, in quantum electrodynamics (QED), an electron appears to be composed of electrons, positrons (anti-electrons) and photons, as one views it at higher resolution, at very short distances. The electron at such short distances has a slightly different electric charge than does the ""dressed electron"" seen at large distances, and this change, or ""running,"" in the value of the electric charge is determined by the renormalization group equation.




![arXiv:1705.06742v1 [cond-mat.quant-gas] 18](http://s1.studyres.com/store/data/015536624_1-695304017ec91e58c90e68ba3242255c-300x300.png)