A PRIMER ON THE ANGULAR MOMENTUM AND PARITY
... the radial equation and usually determines the energy of the level, along with `. In the previous example, the two levels arising form the coupling of ` = 2 and s = 1/2 would be labelled by d3/2 and d5/2 , prefaced by the appropriate n value. Parity Parity is a quantum number that tells you about ho ...
... the radial equation and usually determines the energy of the level, along with `. In the previous example, the two levels arising form the coupling of ` = 2 and s = 1/2 would be labelled by d3/2 and d5/2 , prefaced by the appropriate n value. Parity Parity is a quantum number that tells you about ho ...
The quantum field theory (QFT) dual paradigm in fun
... Where n is the number of quanta of the force field, and & is the field phase. If (!n = 0), & is undefined so that it makes sense to neglect the waveform aspect in favor of the individual, particlelike behavior. On the contrary if (!& = 0), n is undefined because an extremely high number of quanta ar ...
... Where n is the number of quanta of the force field, and & is the field phase. If (!n = 0), & is undefined so that it makes sense to neglect the waveform aspect in favor of the individual, particlelike behavior. On the contrary if (!& = 0), n is undefined because an extremely high number of quanta ar ...
Physics 7802.01 Introduction
... Evidence for conservation of electric charge: Consider reaction e-ve which violates charge conservation but not lepton number or any other quantum number. If the above transition occurs in nature then we should see x-rays from atomic transitions. The absence of such x-rays leads to the limit: te > ...
... Evidence for conservation of electric charge: Consider reaction e-ve which violates charge conservation but not lepton number or any other quantum number. If the above transition occurs in nature then we should see x-rays from atomic transitions. The absence of such x-rays leads to the limit: te > ...
6. Quantum Mechanics II
... which is a sine wave moving in the x direction. Notice that, unlike classical waves, we are not taking the real part of this function. is, in fact, complex. In general, the wave function is complex. But the physically measurable quantities must be real. These include the probability, position, mom ...
... which is a sine wave moving in the x direction. Notice that, unlike classical waves, we are not taking the real part of this function. is, in fact, complex. In general, the wave function is complex. But the physically measurable quantities must be real. These include the probability, position, mom ...
Advanced Quantum Field Theory Lent Term 2013 Hugh Osborn
... Quantum field theory is the basic language of particle physics, and also large parts of statistical physics. Quantum field theory is a subject with many technical complications; we will try to deal with these ‘step by step’. It is, however, not a branch of mathematics yet. The lectures will not be r ...
... Quantum field theory is the basic language of particle physics, and also large parts of statistical physics. Quantum field theory is a subject with many technical complications; we will try to deal with these ‘step by step’. It is, however, not a branch of mathematics yet. The lectures will not be r ...
5.11 Harmonic Oscillator
... Particle in well – how to solve the SE – energy levels – quantization – expectation values – effect of well length – effect of well height – calculating probabilities – compare and contrast with infinite well – classically forbidden ...
... Particle in well – how to solve the SE – energy levels – quantization – expectation values – effect of well length – effect of well height – calculating probabilities – compare and contrast with infinite well – classically forbidden ...
The role of the electromagnetic field in the formation of domains in
... field ψ(x, t). This is a well known story. In the present paper, given the above connection between the matter field and the e.m. field, we wish to discuss, in the frame of QFT, the rôle played by the e.m. field in the locking of the phases of the e.m. modes and of the matter components on an exte ...
... field ψ(x, t). This is a well known story. In the present paper, given the above connection between the matter field and the e.m. field, we wish to discuss, in the frame of QFT, the rôle played by the e.m. field in the locking of the phases of the e.m. modes and of the matter components on an exte ...
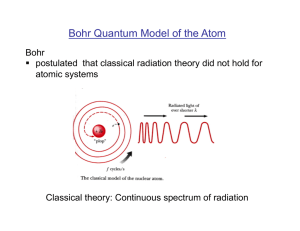
Bohr Quantum Model of the Atom
... § postulated that the electron orbital momentum is quantized Justification of Bohr’s postulates: comparison with experimental observations! ...
... § postulated that the electron orbital momentum is quantized Justification of Bohr’s postulates: comparison with experimental observations! ...
Abstraction as * file
... new lower bound and compute the minimal entropy gain for a broad class of Bosonic Gaussian channels by proving that the infimum is attained on the Gaussian states. The second part of the talk is devoted to the Choi-Jamiolkowski correspondence between channels and states in the infinite-dimensional c ...
... new lower bound and compute the minimal entropy gain for a broad class of Bosonic Gaussian channels by proving that the infimum is attained on the Gaussian states. The second part of the talk is devoted to the Choi-Jamiolkowski correspondence between channels and states in the infinite-dimensional c ...
Here
... the speed of the light. This happens not only when the mass m goes to infinity, but also for a series of point masses moving with an ever growing speed and an ever smaller rest mass such that all the moving masses m keep the same value m. Even in this case the maximum precision grows unlimited with ...
... the speed of the light. This happens not only when the mass m goes to infinity, but also for a series of point masses moving with an ever growing speed and an ever smaller rest mass such that all the moving masses m keep the same value m. Even in this case the maximum precision grows unlimited with ...
From Gravity to Consciousness
... NeuroQuantology 2004;2: 146146-147 Gravity is the inverted, real image of electromagnetism. The force of gravity can be deduced from ratio of relative strength between force of a distant electrically charged object and the force its inverted, real image exerts on an infinitesimal mass of given point ...
... NeuroQuantology 2004;2: 146146-147 Gravity is the inverted, real image of electromagnetism. The force of gravity can be deduced from ratio of relative strength between force of a distant electrically charged object and the force its inverted, real image exerts on an infinitesimal mass of given point ...
Presentation #2
... function of time is called its trajectory. This trajectory is the full description of the motion of the particle Newton's Second Law enables us to calculate the trajectory of a particle in terms of the forces acting on it. Thus the entire history and the entire future of the body's motion, point by ...
... function of time is called its trajectory. This trajectory is the full description of the motion of the particle Newton's Second Law enables us to calculate the trajectory of a particle in terms of the forces acting on it. Thus the entire history and the entire future of the body's motion, point by ...
Giant gravitons: a collective coordinate approach
... Z between the “words” W Main idea: replace Z by Z- in the expansion, so we generate inverse powers of Z- inside traces. ...
... Z between the “words” W Main idea: replace Z by Z- in the expansion, so we generate inverse powers of Z- inside traces. ...
EQUILIBRIUM STATE OF A SELF
... the de Sitter background, let us calculate the evolution of h 2i in the Hartree-Fock approximation following [4,5] (for a recent discussion of this method, see [14]). This approximation is also called Gaussian because the wave functional in the Schrodinger representation is assumed to be Gaussian. ...
... the de Sitter background, let us calculate the evolution of h 2i in the Hartree-Fock approximation following [4,5] (for a recent discussion of this method, see [14]). This approximation is also called Gaussian because the wave functional in the Schrodinger representation is assumed to be Gaussian. ...