Chapter 7 Propositional and Predicate Logic
... Not logically valid, BUT can still be useful. In fact, it models the way humans reason all the time: Every non-flying bird I’ve seen before has been a penguin; hence that non-flying bird must be a penguin. ...
... Not logically valid, BUT can still be useful. In fact, it models the way humans reason all the time: Every non-flying bird I’ve seen before has been a penguin; hence that non-flying bird must be a penguin. ...
PROVING UNPROVABILITY IN SOME NORMAL MODAL LOGIC
... Now, let T = < W, R > be an arbitrarily fixed tree with a set of nodes W = {x1 , . . . , xn }. We attach to these nodes different propositional variables q(x1 ), . . . , q(xn ) or for V short q1 , . . . , qn . This set will be referred as var(T ). Denote χ(xi ) = qi ∧ {¬qj : qj ∈ var(T ), j 6= i}. N ...
... Now, let T = < W, R > be an arbitrarily fixed tree with a set of nodes W = {x1 , . . . , xn }. We attach to these nodes different propositional variables q(x1 ), . . . , q(xn ) or for V short q1 , . . . , qn . This set will be referred as var(T ). Denote χ(xi ) = qi ∧ {¬qj : qj ∈ var(T ), j 6= i}. N ...
Lecture 16 Notes
... complete with respect to “exploding” Kripke models. His proof is constructive. As yet it is not clear how to use his models in a computational way, unlike the situation for uniform evidence semantics. ...
... complete with respect to “exploding” Kripke models. His proof is constructive. As yet it is not clear how to use his models in a computational way, unlike the situation for uniform evidence semantics. ...
HISTORY OF LOGIC
... – Considered to be the father of Analytic Philosophy. – His Objective was demonstrating that arithmetic is identical with logic. – He invented axiomatic predicate logic and quantified variables, which solved the problem of multiple generality. ...
... – Considered to be the father of Analytic Philosophy. – His Objective was demonstrating that arithmetic is identical with logic. – He invented axiomatic predicate logic and quantified variables, which solved the problem of multiple generality. ...
Lambda Calculus and Functional Programming
... single function definition scheme. It was introduced in the 1930s by Alonzo Church as a way of formalizing the concept of effective computability. The λ-calculus is universal in the sense that any computable function can be expressed and evaluated using this formalism. It is thus equivalent to Turin ...
... single function definition scheme. It was introduced in the 1930s by Alonzo Church as a way of formalizing the concept of effective computability. The λ-calculus is universal in the sense that any computable function can be expressed and evaluated using this formalism. It is thus equivalent to Turin ...
The Lambda Calculus: a minimal ML?
... Curry and his colleagues (see Curry et al. (1958,1972)). Roughly, the goal of combinator logic was to develop rules of logic that were variable-free. Expression of functions in combinatory logic used an alphabet of a fixed set of combinators, essentially functional terms that operated on other terms ...
... Curry and his colleagues (see Curry et al. (1958,1972)). Roughly, the goal of combinator logic was to develop rules of logic that were variable-free. Expression of functions in combinatory logic used an alphabet of a fixed set of combinators, essentially functional terms that operated on other terms ...
Artificial Intelligence
... • To express the idea that everyone likes cheese, we might say: (∀x)(P(x)→L(x, C)) • The symbol ∀ is read “for all,” so the statement above could be read as “for every x it is true that if property P holds for x, then the relationship L holds between x and C,” or in plainer English: “every x that is ...
... • To express the idea that everyone likes cheese, we might say: (∀x)(P(x)→L(x, C)) • The symbol ∀ is read “for all,” so the statement above could be read as “for every x it is true that if property P holds for x, then the relationship L holds between x and C,” or in plainer English: “every x that is ...
PDF
... theorem, and the only if part is the completeness theorem. We will prove the two parts separately here. We begin with the easier one: Theorem 1. Propositional logic is sound with respect to truth-value semantics. Proof. Basically, we need to show that every axiom is a tautology, and that the inferen ...
... theorem, and the only if part is the completeness theorem. We will prove the two parts separately here. We begin with the easier one: Theorem 1. Propositional logic is sound with respect to truth-value semantics. Proof. Basically, we need to show that every axiom is a tautology, and that the inferen ...
HW-04 due 02/10
... (,), represent in predicate logic the following sentences, write the negation of the predicate expression and translate back to English a. Some classes are difficult and boring. b. Difficult classes are not boring. c. No classes are difficult and boring ...
... (,), represent in predicate logic the following sentences, write the negation of the predicate expression and translate back to English a. Some classes are difficult and boring. b. Difficult classes are not boring. c. No classes are difficult and boring ...
Functional PLs
... Functional languages try to model mathematical functions as much as possible. ...
... Functional languages try to model mathematical functions as much as possible. ...
Lecture10 - CIS @ UPenn
... • Can I pass a function as an argument to another function • YES! • The first time you see this, it looks crazy • Just start thinking of a function as a machine that turns ...
... • Can I pass a function as an argument to another function • YES! • The first time you see this, it looks crazy • Just start thinking of a function as a machine that turns ...
Functional Programming Languages
... The values of the parameters are substituted into the function body The function body is evaluated The value of the last expression in the body is the value of the function ...
... The values of the parameters are substituted into the function body The function body is evaluated The value of the last expression in the body is the value of the function ...
fund
... Formal system with three parts • Notation for function expressions • Proof system for equations • Calculation rules called reduction ...
... Formal system with three parts • Notation for function expressions • Proof system for equations • Calculation rules called reduction ...
Lecture10
... The 3 argument version of the reduce function • We have already seem reduce(function, list) • There is a 3 argument variant which is • Reduce(function, list, identity element/first element for the process ...
... The 3 argument version of the reduce function • We have already seem reduce(function, list) • There is a 3 argument variant which is • Reduce(function, list, identity element/first element for the process ...
CS 170 * Intro to Programming for Scientists and Engineers
... These symbols are not variables – they are like the names bound by Java’s final declarations ...
... These symbols are not variables – they are like the names bound by Java’s final declarations ...
Functional Programming
... What is a Functional Language? Opinions differ, and it is difficult to give a precise definition, but generally speaking: Functional programming is style of programming in which the basic method of computation is the application of functions to arguments; ...
... What is a Functional Language? Opinions differ, and it is difficult to give a precise definition, but generally speaking: Functional programming is style of programming in which the basic method of computation is the application of functions to arguments; ...
doc
... I believe that mainly this metric can be used to infer how concise the design is. In theory a succinct design should have better clarity, as there is less code to understand. However, although functional code can fit into much fewer lines, it is still possible to write bad code that is just as hard ...
... I believe that mainly this metric can be used to infer how concise the design is. In theory a succinct design should have better clarity, as there is less code to understand. However, although functional code can fit into much fewer lines, it is still possible to write bad code that is just as hard ...
Fundamentals
... Functional programming: Example 1 Devise a representation for stacks and implementations for functions push (elt, stk) returns stack with elt on top of stk ...
... Functional programming: Example 1 Devise a representation for stacks and implementations for functions push (elt, stk) returns stack with elt on top of stk ...
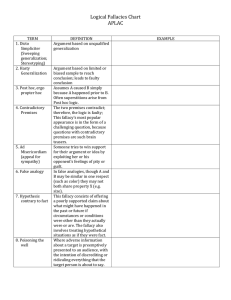
Logical Fallacies Chart APLAC TERM DEFINITION EXAMPLE 1
... This fallacy's most popular appearance is in the form of a challenging question, because questions with contradictory premises are such brain teasers. Someone tries to win support for their argument or idea by exploiting her or his opponent's feelings of pity or guilt. In false analogies, though A a ...
... This fallacy's most popular appearance is in the form of a challenging question, because questions with contradictory premises are such brain teasers. Someone tries to win support for their argument or idea by exploiting her or his opponent's feelings of pity or guilt. In false analogies, though A a ...