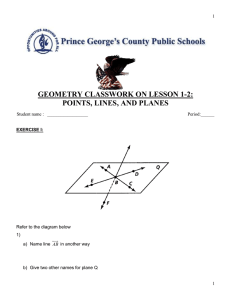
Unit 1 : Point, Line and Plane Geometry Definitions (1.21.6) p.1050
... Measure of angle ABC: written as m
... Measure of angle ABC: written as m
Unit 3 Parallel and Perpendicular Lines
... A pair of alternate exterior angles is __________________, then the two lines are ___________________. A pair of alternate interior angles is ___________________, then the lines are __________________. A pair of consecutive interior angles is ________________________, then the lines are ______ ...
... A pair of alternate exterior angles is __________________, then the two lines are ___________________. A pair of alternate interior angles is ___________________, then the lines are __________________. A pair of consecutive interior angles is ________________________, then the lines are ______ ...
Sharing Joints, in Moderation A Grounshaking Clash between
... (lines forming a fixed angle with the z-axis) in space and their joints is O(n3/2 log1/2 n) A very special case of a much harder problem he worked on, related to distinct distances in the plane coming up soon! ...
... (lines forming a fixed angle with the z-axis) in space and their joints is O(n3/2 log1/2 n) A very special case of a much harder problem he worked on, related to distinct distances in the plane coming up soon! ...
Logic and Incidence Geometry
... if they do not meet in A , i.e., they are parallel in A , then they meet at the point [l] (= [m]) in A ∗ . For an ordinary line l in A and l∞ , they meet at the point [l] in A ∗ . Example 7 (A model of real projective plane). Let S be a sphere centered at the origin O of our 3-dimension Euclidean sp ...
... if they do not meet in A , i.e., they are parallel in A , then they meet at the point [l] (= [m]) in A ∗ . For an ordinary line l in A and l∞ , they meet at the point [l] in A ∗ . Example 7 (A model of real projective plane). Let S be a sphere centered at the origin O of our 3-dimension Euclidean sp ...
Perspective (graphical)

Perspective (from Latin: perspicere to see through) in the graphic arts is an approximate representation, on a flat surface (such as paper), of an image as it is seen by the eye. The two most characteristic features of perspective are that objects are smaller as their distance from the observer increases; and that they are subject to foreshortening, meaning that an object's dimensions along the line of sight are shorter than its dimensions across the line of sight.Italian Renaissance painters including Paolo Uccello, Piero della Francesca and Luca Pacoima studied linear perspective, wrote treatises on it, and incorporated it into their artworks, thus contributing to the mathematics of art.