3-6-17 math - Trousdale County Schools
... plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not. 4. Develop definitions of rotations, reflections, an ...
... plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not. 4. Develop definitions of rotations, reflections, an ...
Cohomological equations and invariant distributions on a compact
... (left translation by a). We give necessary and sufficient conditions for the existence of solutions of the cohomological equation f − f ◦ γ = g on the Fréchet space C ∞ (G) of complex C ∞ functions on G. ii) When G is the torus Tn , we compute explicitly the distributions on Tn invariant by an affi ...
... (left translation by a). We give necessary and sufficient conditions for the existence of solutions of the cohomological equation f − f ◦ γ = g on the Fréchet space C ∞ (G) of complex C ∞ functions on G. ii) When G is the torus Tn , we compute explicitly the distributions on Tn invariant by an affi ...
Geometry Curriculum The length of part of a circle`s circumference
... Learning Outcomes (CCSS) G.C.1 Prove that all circles are similar. G.C.2 Identify and describe relationships among inscribed angles, radii, and chords. Include the relationship between central, inscribed, and circumscribed angles; inscribed angles on a diameter are right angles; the radius of a circ ...
... Learning Outcomes (CCSS) G.C.1 Prove that all circles are similar. G.C.2 Identify and describe relationships among inscribed angles, radii, and chords. Include the relationship between central, inscribed, and circumscribed angles; inscribed angles on a diameter are right angles; the radius of a circ ...
Geometry - Carl Junction Schools
... 4c. Prove theorems about triangles. A line parallel to one side of a triangle divides the other two proportionally and conversely the Pythagorean Theorem proved used triangle similarity. 4d. Use congruence and similarity criteria for triangles to solve problems and to prove relationships in geometri ...
... 4c. Prove theorems about triangles. A line parallel to one side of a triangle divides the other two proportionally and conversely the Pythagorean Theorem proved used triangle similarity. 4d. Use congruence and similarity criteria for triangles to solve problems and to prove relationships in geometri ...
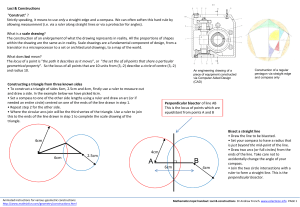
Constructions with ruler and compass Congruence tests for triangles
... For the first part, our recipe can use only the following operations: Draw a line through two given points Draw a circle with center at a given point and given radius Find and label on the figure intersection points of already constructed lines and circles. For the second part, we will frequen ...
... For the first part, our recipe can use only the following operations: Draw a line through two given points Draw a circle with center at a given point and given radius Find and label on the figure intersection points of already constructed lines and circles. For the second part, we will frequen ...
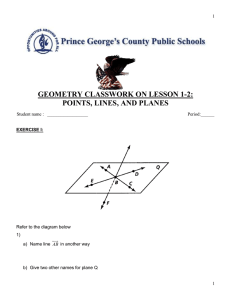
Vocab(1). - Wiki6Math
... The set of points between points P and Q in a plane and the infinite number of points that continue beyond the points. PQ ...
... The set of points between points P and Q in a plane and the infinite number of points that continue beyond the points. PQ ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.