SLV RT3 - Within and Around - Integrated Math III Unit 2
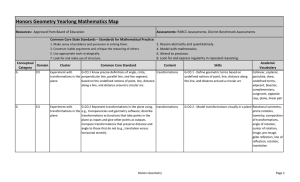
... Critical Language: includes the Academic and Technical vocabulary, semantics, and discourse which are particular to and necessary for accessing a given discipline. EXAMPLE: A student in Language Arts can demonstrate the ability to apply and comprehend critical language through the following statemen ...
... Critical Language: includes the Academic and Technical vocabulary, semantics, and discourse which are particular to and necessary for accessing a given discipline. EXAMPLE: A student in Language Arts can demonstrate the ability to apply and comprehend critical language through the following statemen ...
Document
... Properties of Circles The measure of a central angle is two times the measure of the inscribed angle that intercepts the same arc. B A ...
... Properties of Circles The measure of a central angle is two times the measure of the inscribed angle that intercepts the same arc. B A ...
8-5: Butterflies, Pinwheels, and Wallpaper
... 1. How would you explain what it means for two geometric shapes to be similar using 1a. everyday words that most people could understand? 1b. technical terms of mathematics? ...
... 1. How would you explain what it means for two geometric shapes to be similar using 1a. everyday words that most people could understand? 1b. technical terms of mathematics? ...
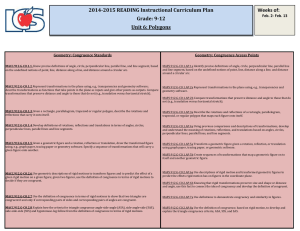
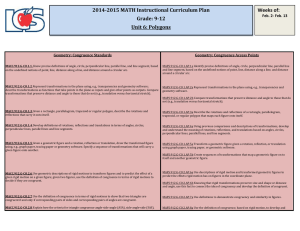
Honors Geometry Yearlong Curriculum Map
... similarity transformations (Dilations) G-SRT.1a A dilation takes a line not passing through the similarity center of the dilation to a parallel line, and leaves a transformations line passing through the center unchanged. (Dilations) G-SRT.1b The dilation of a line segment is longer or similarity sh ...
... similarity transformations (Dilations) G-SRT.1a A dilation takes a line not passing through the similarity center of the dilation to a parallel line, and leaves a transformations line passing through the center unchanged. (Dilations) G-SRT.1b The dilation of a line segment is longer or similarity sh ...
Honors Geometry
... _________1. A(-4,0) and B(-2,4). Find the coordinates of the midpoint of AB . _________2. Find AB in #1. _________3. The midpoint of RS is U. If U(-3, 5) and S(2, 13) Find the coordinates of R. _________4. Find the points of intersection for: a) y = 2x and 3x + y = 10 b) 4x + 2y = -10 and 3x + y = - ...
... _________1. A(-4,0) and B(-2,4). Find the coordinates of the midpoint of AB . _________2. Find AB in #1. _________3. The midpoint of RS is U. If U(-3, 5) and S(2, 13) Find the coordinates of R. _________4. Find the points of intersection for: a) y = 2x and 3x + y = 10 b) 4x + 2y = -10 and 3x + y = - ...
15 the geometry of whales and ants non
... do. Most importantly, it is a geometry of negative curvature. This means that lines that start out parallel tend to move farther and farther apart. ...
... do. Most importantly, it is a geometry of negative curvature. This means that lines that start out parallel tend to move farther and farther apart. ...
Geometry - missmillermath
... 5. Notebooks will be graded near the end of each marking period. Students will be given at least 2 days notice of when they will be checked. If a notebook is not handed in by 3 p.m. on the designated day the student will be penalized 5 points per day for every day that it is late. (This does not inc ...
... 5. Notebooks will be graded near the end of each marking period. Students will be given at least 2 days notice of when they will be checked. If a notebook is not handed in by 3 p.m. on the designated day the student will be penalized 5 points per day for every day that it is late. (This does not inc ...
Geometry Level 2 Ms. Sheppard-Brick 617-596
... 14) Conjecture: If two circles touch each other, then one circle is inside the other circle. Directions: Use the diagram at right for problems 15 – 20 15) Name three points that are collinear. 16) Name four points that are coplanar. 17) Name two lines that are coplanar. 18) Name three points that ar ...
... 14) Conjecture: If two circles touch each other, then one circle is inside the other circle. Directions: Use the diagram at right for problems 15 – 20 15) Name three points that are collinear. 16) Name four points that are coplanar. 17) Name two lines that are coplanar. 18) Name three points that ar ...
Mathematics - Renton School District
... Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc. G-CO.2 Represent transformations in the plane using, e.g., transparencies and geometry software; d ...
... Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc. G-CO.2 Represent transformations in the plane using, e.g., transparencies and geometry software; d ...
Chapter 10: Angles and Triangles
... • Formed by two intersecting lines: vertically opposite, adjacent • Formed by a transversal intersecting two other lines: alternate interior, alternate exterior, corresponding ...
... • Formed by two intersecting lines: vertically opposite, adjacent • Formed by a transversal intersecting two other lines: alternate interior, alternate exterior, corresponding ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.