Definitions Synthetic Geometry- the study of description of points
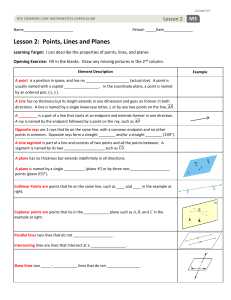
... 2. Description of a point- A point is an exact location 3. Description of a line- A line is a set of points extending in both directions containing the shortest path between any two points on it. 4. Distance- Between two points on a coordinatized line is the absolute value of the difference of their ...
... 2. Description of a point- A point is an exact location 3. Description of a line- A line is a set of points extending in both directions containing the shortest path between any two points on it. 4. Distance- Between two points on a coordinatized line is the absolute value of the difference of their ...
Geometry
... from the perspective of geometric transformation. Fundamental are the rigid motions: translations, rotations, reflections, and combinations of these, all of which are here assumed to preserve distance and angles (and therefore shapes generally). Reflections and rotations each explain a particular type ...
... from the perspective of geometric transformation. Fundamental are the rigid motions: translations, rotations, reflections, and combinations of these, all of which are here assumed to preserve distance and angles (and therefore shapes generally). Reflections and rotations each explain a particular type ...
p. 1 Madison County Schools Suggested Geometry Pacing Guide
... using similarity transformations the meaning of similarity for triangles as the equality of all corresponding pairs of angles and the proportionality of all corresponding pairs of sides. Use the properties of similarity transformations to establish the AA criterion for two triangles to be similar. P ...
... using similarity transformations the meaning of similarity for triangles as the equality of all corresponding pairs of angles and the proportionality of all corresponding pairs of sides. Use the properties of similarity transformations to establish the AA criterion for two triangles to be similar. P ...
Unit 01-Vocab-Blank SE G2A
... Points or lines that lie on the same plane are called coplanar. A line segment is a straight path that begins at one point and ends at another point. It has a finite length A straight path that has a beginning but no end is called a ray. A point that begins or ends a line segment or begins a ray is ...
... Points or lines that lie on the same plane are called coplanar. A line segment is a straight path that begins at one point and ends at another point. It has a finite length A straight path that has a beginning but no end is called a ray. A point that begins or ends a line segment or begins a ray is ...
Trigonometry - Nayland Maths
... Rotational symmetry A shape has rotational symmetry if it can be rotated on to itself. Scale factor A number used as the factor for dilation, enlargement (or size transformation), and scale drawings. Scalene triangle A triangle in which no sides are congruent. Sector Part of a circle bounded by an a ...
... Rotational symmetry A shape has rotational symmetry if it can be rotated on to itself. Scale factor A number used as the factor for dilation, enlargement (or size transformation), and scale drawings. Scalene triangle A triangle in which no sides are congruent. Sector Part of a circle bounded by an a ...
Glossary for Module 5 Term Definition Alternate Exterior Angles Any
... A line divides a plane into two sides. If two items are on the same side then line is not between them. To create free hand with only a pencil. A rectangle with all sides congruent. Side – Side – Side An angle that measures 180°. Two angles the sum of whose measures is 180 degrees. A general stateme ...
... A line divides a plane into two sides. If two items are on the same side then line is not between them. To create free hand with only a pencil. A rectangle with all sides congruent. Side – Side – Side An angle that measures 180°. Two angles the sum of whose measures is 180 degrees. A general stateme ...
Marking Period 1 Vocab
... from a vertex of a triangle to the opposite side or to the line that contains the ...
... from a vertex of a triangle to the opposite side or to the line that contains the ...
Unit 2 Lines and Transformations Geometry
... outside of school? Where do you see examples of this? • Rigid transformations preserve a figure’s size and • What are the big understandings behind “slope”? shape or distance and angle measure and, thus, may • Based on the definition of parallel lines as two lines that be used to prove the congruenc ...
... outside of school? Where do you see examples of this? • Rigid transformations preserve a figure’s size and • What are the big understandings behind “slope”? shape or distance and angle measure and, thus, may • Based on the definition of parallel lines as two lines that be used to prove the congruenc ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.