Name___________________ AUDITORY Directions: For the next
... Find the foldable and fill in the blanks with the important ideas surrounding “Transformations.” Be sure to include pictures, drawings, and examples! Once complete, see Ms. Webber or Ms. Rohrlack to learn how to fold this so it looks like an accordion. ...
... Find the foldable and fill in the blanks with the important ideas surrounding “Transformations.” Be sure to include pictures, drawings, and examples! Once complete, see Ms. Webber or Ms. Rohrlack to learn how to fold this so it looks like an accordion. ...
Polygons and their Properties 4.1. Polygons
... 6. Recall the theorem about the constructible regular polygons mentioned in Chapter Three that was proved by Gauss. List all regular polygons with fewer than 50 sides that can be constructed with compass and straightedge. 7. Using Sketchpad we are able to construct shapes with rotational symmetries. ...
... 6. Recall the theorem about the constructible regular polygons mentioned in Chapter Three that was proved by Gauss. List all regular polygons with fewer than 50 sides that can be constructed with compass and straightedge. 7. Using Sketchpad we are able to construct shapes with rotational symmetries. ...
Solution
... each electron in each microstate in the table. (Use the format mlms. That is a spin -½ electron in an s orbital would be written as 0-) Provide the term symbols representing the states constructed from the table. Make sure to include the spin-orbit coupling quantum number, J. Then determine which of ...
... each electron in each microstate in the table. (Use the format mlms. That is a spin -½ electron in an s orbital would be written as 0-) Provide the term symbols representing the states constructed from the table. Make sure to include the spin-orbit coupling quantum number, J. Then determine which of ...
INTRO Slide Show
... straight lines, and if one of them cut the circle and the other touch it, the rectangle contained by the whole of the straight line which cuts the circle and the straight line intercepted on it outside between the point and the convex circumference will be equal to the square on the tangent. ...
... straight lines, and if one of them cut the circle and the other touch it, the rectangle contained by the whole of the straight line which cuts the circle and the straight line intercepted on it outside between the point and the convex circumference will be equal to the square on the tangent. ...
Euclid of Alexandria: Elementary Geometry
... right angle, parallel line, etc.), (2) postulates (ex. to draw a line, circle, all right angles are equal, 5th post.1 ), and (3) common notions (equals to equals are equal, the whole is greater than the individual parts, etc.) The propositions start with a series of construction “problems” and devel ...
... right angle, parallel line, etc.), (2) postulates (ex. to draw a line, circle, all right angles are equal, 5th post.1 ), and (3) common notions (equals to equals are equal, the whole is greater than the individual parts, etc.) The propositions start with a series of construction “problems” and devel ...
Angle and Regular Polygon Review
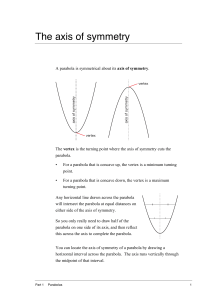
... A quarter circle has one-fourth the degrees of a full circle. Such a 90 degree angle is called a right angle. It is often shown with a small square corner near the vertex of a right angle. ...
... A quarter circle has one-fourth the degrees of a full circle. Such a 90 degree angle is called a right angle. It is often shown with a small square corner near the vertex of a right angle. ...
Symplectic Topology
... such a pairing. Symplectic geometry is the geometry of a non-degenerate skew-symmetric bilinear form, which moreover we insist is “locally constant” as we vary from tangent space to tangent space. Formally, fix the skew form ...
... such a pairing. Symplectic geometry is the geometry of a non-degenerate skew-symmetric bilinear form, which moreover we insist is “locally constant” as we vary from tangent space to tangent space. Formally, fix the skew form ...
NEKSDC CCSSM HS Geometry
... • Synthetic Geometry is the branch of geometry which makes use of axioms, theorems, and logical arguments to draw conclusions about shapes and solve problems • Analytical Geometry places shapes on the coordinate plane, allowing shapes to defined by algebraic equations, which can be manipulated to dr ...
... • Synthetic Geometry is the branch of geometry which makes use of axioms, theorems, and logical arguments to draw conclusions about shapes and solve problems • Analytical Geometry places shapes on the coordinate plane, allowing shapes to defined by algebraic equations, which can be manipulated to dr ...
Parallelogram
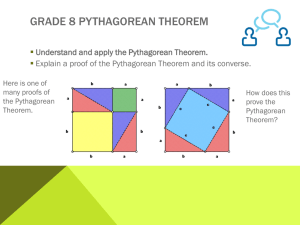
... II. Find a relation from the diagram that is an example of the given mathematical reason. 1. In a parallelogram the diagonals bisect each other. ...
... II. Find a relation from the diagram that is an example of the given mathematical reason. 1. In a parallelogram the diagonals bisect each other. ...
circle… - cmasemath
... All points on my edge are the same distance to my center. If you know the distance from my center to the edge you can know so much more about me…diameter, circumference, and area. No matter my size, my diameter is equal to the ratio of my circumference to Pi. What am I? ...
... All points on my edge are the same distance to my center. If you know the distance from my center to the edge you can know so much more about me…diameter, circumference, and area. No matter my size, my diameter is equal to the ratio of my circumference to Pi. What am I? ...
String-Matching Problem
... The probability of a false positive hit for a random input is 1/q The expected number of false positive hits is O( n/q ) The expected run time of Rabin-Karp is O( n ) + O( m ( v + n/q ))) if v is the number of valid shifts (hits) If we choose q ≥ m and have only a constant number of hits, then ...
... The probability of a false positive hit for a random input is 1/q The expected number of false positive hits is O( n/q ) The expected run time of Rabin-Karp is O( n ) + O( m ( v + n/q ))) if v is the number of valid shifts (hits) If we choose q ≥ m and have only a constant number of hits, then ...
Stained Glass - Noyce Foundation
... They should have opportunities to draw in lines of symmetry and use mirrors to check for lines of symmetry. They should be able to work with a variety of shapes and designs, where the lines of symmetry are not always or limited to the horizontal and vertical. Students thinking about symmetry should ...
... They should have opportunities to draw in lines of symmetry and use mirrors to check for lines of symmetry. They should be able to work with a variety of shapes and designs, where the lines of symmetry are not always or limited to the horizontal and vertical. Students thinking about symmetry should ...
Foundation Student Book Chapter 6
... Congruent shapes are shapes that are exactly the same size and exactly the same shape. A tessallation is when a shape is drawn over and over again so that it covers an area without any gaps or overlaps. There are several key words associated with circles: circumference, diameter, radius, tangent, ch ...
... Congruent shapes are shapes that are exactly the same size and exactly the same shape. A tessallation is when a shape is drawn over and over again so that it covers an area without any gaps or overlaps. There are several key words associated with circles: circumference, diameter, radius, tangent, ch ...
Foundation Student Book Chapter 6
... Congruent shapes are shapes that are exactly the same size and exactly the same shape. A tessallation is when a shape is drawn over and over again so that it covers an area without any gaps or overlaps. There are several key words associated with circles: circumference, diameter, radius, tangent, ch ...
... Congruent shapes are shapes that are exactly the same size and exactly the same shape. A tessallation is when a shape is drawn over and over again so that it covers an area without any gaps or overlaps. There are several key words associated with circles: circumference, diameter, radius, tangent, ch ...
Mirror symmetry (string theory)
In algebraic geometry and theoretical physics, mirror symmetry is a relationship between geometric objects called Calabi–Yau manifolds. The term refers to a situation where two Calabi–Yau manifolds look very different geometrically but are nevertheless equivalent when employed as extra dimensions of string theory.Mirror symmetry was originally discovered by physicists. Mathematicians became interested in this relationship around 1990 when Philip Candelas, Xenia de la Ossa, Paul Green, and Linda Parkes showed that it could be used as a tool in enumerative geometry, a branch of mathematics concerned with counting the number of solutions to geometric questions. Candelas and his collaborators showed that mirror symmetry could be used to count rational curves on a Calabi–Yau manifold, thus solving a longstanding problem. Although the original approach to mirror symmetry was based on physical ideas that were not understood in a mathematically precise way, some of its mathematical predictions have since been proven rigorously.Today mirror symmetry is a major research topic in pure mathematics, and mathematicians are working to develop a mathematical understanding of the relationship based on physicists' intuition. Mirror symmetry is also a fundamental tool for doing calculations in string theory, and it has been used to understand aspects of quantum field theory, the formalism that physicists use to describe elementary particles. Major approaches to mirror symmetry include the homological mirror symmetry program of Maxim Kontsevich and the SYZ conjecture of Andrew Strominger, Shing-Tung Yau, and Eric Zaslow.