Lecture 4
... homeomorphic to S 2 . Let η1 denote the quotient map I 2 −→ S 2 which collapses the boundary to a singleton and likewise let η2 : S 1 × S 1 −→ (S 1 × S 1 )/(S 1 ∨ S 1 ) be the quotient map. The map φ : S 1 × S 1 −→ S 2 given by the prescription φ(exp(2πix), exp(2πiy)) = η1 (x, y) is well-defined and ...
... homeomorphic to S 2 . Let η1 denote the quotient map I 2 −→ S 2 which collapses the boundary to a singleton and likewise let η2 : S 1 × S 1 −→ (S 1 × S 1 )/(S 1 ∨ S 1 ) be the quotient map. The map φ : S 1 × S 1 −→ S 2 given by the prescription φ(exp(2πix), exp(2πiy)) = η1 (x, y) is well-defined and ...
1. Introduction. General Topology is a framework inside which some
... space is homogeneous [15]. The next question remains open: Problem 2.3. [6] Is every diagonal-flexible space homogeneous? ...
... space is homogeneous [15]. The next question remains open: Problem 2.3. [6] Is every diagonal-flexible space homogeneous? ...
Toposym Kanpur - DML-CZ
... C. Chevalley and O. Frink [5] proved that an arbitrary product of H-closed spaces is H-closed. H-closed spaces play an important role in the theory of minimal-Hausdorff spaces. In this direction, work has been done by M. Katetov [17, 18], A. Ramanathan [28, 29], F. Obreanu [23, 24] and others. It is ...
... C. Chevalley and O. Frink [5] proved that an arbitrary product of H-closed spaces is H-closed. H-closed spaces play an important role in the theory of minimal-Hausdorff spaces. In this direction, work has been done by M. Katetov [17, 18], A. Ramanathan [28, 29], F. Obreanu [23, 24] and others. It is ...
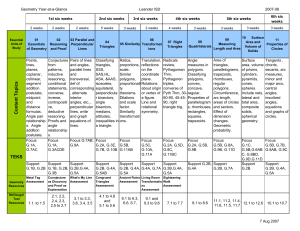
1 Key Terms Angle - the space (usually measured in degrees
... Angle - the space (usually measured in degrees) between two intersecting lines or surfaces at or close to the point where they meet. Arc – A segment of the circumference of a circle. A Major Arc is the longer of the two arcs between two points on a circle. A Minor Arc is the shorter of the two arcs ...
... Angle - the space (usually measured in degrees) between two intersecting lines or surfaces at or close to the point where they meet. Arc – A segment of the circumference of a circle. A Major Arc is the longer of the two arcs between two points on a circle. A Minor Arc is the shorter of the two arcs ...
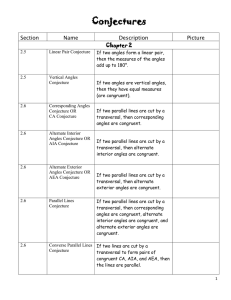
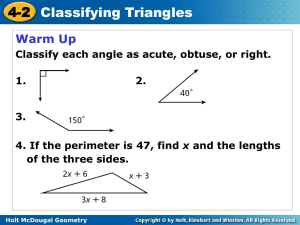
Unit Two Reasoning, Justification And Proof 18 Hours
... terms) and ground-rules (postulates) to go by. These are simply accepted as being true without proof. These assumptions differ from Euclidean to non-Euclidean geometries. Examples of undefined terms are: point, line and plane. Examples of postulates are: For any two points there is exactly one line ...
... terms) and ground-rules (postulates) to go by. These are simply accepted as being true without proof. These assumptions differ from Euclidean to non-Euclidean geometries. Examples of undefined terms are: point, line and plane. Examples of postulates are: For any two points there is exactly one line ...