Regular
... standards for Geometry are based upon these new standards; however, during this transition year students will be assessed using the Geometry EOC for Geometry aligned with the Next Generation Sunshine State Standards. For this reason, instruction should include a blend of the CCSS and the NGSSS. ...
... standards for Geometry are based upon these new standards; however, during this transition year students will be assessed using the Geometry EOC for Geometry aligned with the Next Generation Sunshine State Standards. For this reason, instruction should include a blend of the CCSS and the NGSSS. ...
Free Topological Groups - Universidad Complutense de Madrid
... topologies on F (X ) with the same properties, we get the required “free” topological group topology on F (X ). This finishes the existence proof in the non-Abelian case. A similar argument, with obvious modifications, implies the existence of the free Abelian topological group A(X ) over a Tychonof ...
... topologies on F (X ) with the same properties, we get the required “free” topological group topology on F (X ). This finishes the existence proof in the non-Abelian case. A similar argument, with obvious modifications, implies the existence of the free Abelian topological group A(X ) over a Tychonof ...
Separated and proper morphisms
... The notions of separatedness and properness are the algebraic geometry analogues of the Hausdorff condition and compactness in topology. For varieties over the complex numbers, it is possible to use the “analytic topology” inherited from the usual topology on C in place of the Zariski topology, and ...
... The notions of separatedness and properness are the algebraic geometry analogues of the Hausdorff condition and compactness in topology. For varieties over the complex numbers, it is possible to use the “analytic topology” inherited from the usual topology on C in place of the Zariski topology, and ...
REPRESENTATIONS OF DYNAMICAL SYSTEMS ON BANACH
... systems they can be characterized as those G-systems where the family of maps {p : X → X}p∈E(X) is a fragmented family (see Fact 3.5 and Definition 2.7 below). In particular, every individual p : X → X is a fragmented map. Thus, these enveloping semigroup characterizations yield a natural hierarchy ...
... systems they can be characterized as those G-systems where the family of maps {p : X → X}p∈E(X) is a fragmented family (see Fact 3.5 and Definition 2.7 below). In particular, every individual p : X → X is a fragmented map. Thus, these enveloping semigroup characterizations yield a natural hierarchy ...
Uniform maps into normed spaces
... any coreflection, and proved that property (1) is coreflective. This means that in the setting of this note for each uniform space X there exists a finer space mX with property (1) such that if / : Y -^ X is uniformly continuous, and if Y has (1), then/ : Y -> mX is uniformly continuous. The proof o ...
... any coreflection, and proved that property (1) is coreflective. This means that in the setting of this note for each uniform space X there exists a finer space mX with property (1) such that if / : Y -^ X is uniformly continuous, and if Y has (1), then/ : Y -> mX is uniformly continuous. The proof o ...
Flatland 2: Sphereland
... The king of Lineland cannot change left and right by remaining in Lineland. Puncto pulls him out and puts him back after accidentally rotating him. That is how he gets his orientation changed. The same thing happens in Flatland. Hex wants Spherius to flip the orientation of the ship, which he can do ...
... The king of Lineland cannot change left and right by remaining in Lineland. Puncto pulls him out and puts him back after accidentally rotating him. That is how he gets his orientation changed. The same thing happens in Flatland. Hex wants Spherius to flip the orientation of the ship, which he can do ...
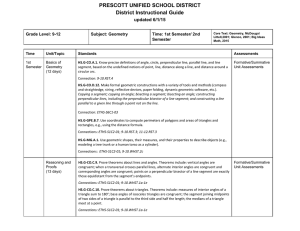
Geometry - Prescott Unified School District
... Represent transformations in the plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not (e.g., translation v ...
... Represent transformations in the plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not (e.g., translation v ...
Math 396. Quotients by group actions Many important manifolds are
... first is most succinctly described with the notation x.(gg 0 ) = (x.g).g 0 whereas the second is most succinctly described with the notation (gg 0 ).x = g.(g 0 .x). Hence, this second possibility is called a left action. Of course, nothing prevents us from using the notation g.x for right actions, b ...
... first is most succinctly described with the notation x.(gg 0 ) = (x.g).g 0 whereas the second is most succinctly described with the notation (gg 0 ).x = g.(g 0 .x). Hence, this second possibility is called a left action. Of course, nothing prevents us from using the notation g.x for right actions, b ...
Course 421: Algebraic Topology Section 1
... exist strictly positive real numbers δ1 , δ2 , . . . , δk such that BX (x, δj ) ⊂ Vj for j = 1, 2, . . . , k. Let δ be the minimum of δ1 , δ2 , . . . , δk . Then δ > 0. (This is where we need the fact that we are dealing with a finite collection of open sets.) Moreover BX (x, δ) ⊂ BX (x, δj ) ⊂ Vj f ...
... exist strictly positive real numbers δ1 , δ2 , . . . , δk such that BX (x, δj ) ⊂ Vj for j = 1, 2, . . . , k. Let δ be the minimum of δ1 , δ2 , . . . , δk . Then δ > 0. (This is where we need the fact that we are dealing with a finite collection of open sets.) Moreover BX (x, δ) ⊂ BX (x, δj ) ⊂ Vj f ...
INTRODUCTION TO MANIFOLDS - PART 1/3 Contents 1. What is Algebraic Topology?
... Here is a loose introduction to Algebraic topology. Checking whether two topological spaces are homeomorphic is a difficult problem in general. In Algebraic Topology, we make a compromise and consider the simpler problem of checking the equivalence of spaces under a weaker notion called homotopy. Roug ...
... Here is a loose introduction to Algebraic topology. Checking whether two topological spaces are homeomorphic is a difficult problem in general. In Algebraic Topology, we make a compromise and consider the simpler problem of checking the equivalence of spaces under a weaker notion called homotopy. Roug ...
O-minimal structures
... 2.10.1 Proof of (Un ). We can assume that, for every x ∈ Rn−1!, Ax is contained in (−1, 1) (we can replace A with its image by (x, y) #→ (x, y/ 1 + y 2 )). For x ∈ Rn−1 with Ax %= ∅, define fi (x) by Ax = {f1 (x), · · · , f#(Ax ) (x)}, f1 (x) < · · · < f#(Ax ) (x). Note that, for each i ∈ {1, 2, · · ...
... 2.10.1 Proof of (Un ). We can assume that, for every x ∈ Rn−1!, Ax is contained in (−1, 1) (we can replace A with its image by (x, y) #→ (x, y/ 1 + y 2 )). For x ∈ Rn−1 with Ax %= ∅, define fi (x) by Ax = {f1 (x), · · · , f#(Ax ) (x)}, f1 (x) < · · · < f#(Ax ) (x). Note that, for each i ∈ {1, 2, · · ...