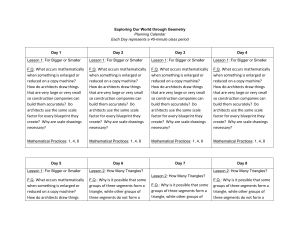
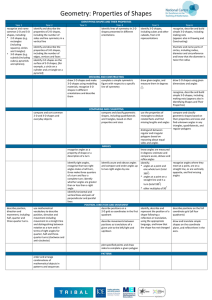
12-1 Define and Use Sequences and Series
... Ex 4: Solve ΔABC with A = 30°, a = 10, and b = 15. ---First make a sketch. Because b sin A = _____________ = _______ , and 7.5 < 10 < 15 (h < a < b), two triangles can be formed. ...
... Ex 4: Solve ΔABC with A = 30°, a = 10, and b = 15. ---First make a sketch. Because b sin A = _____________ = _______ , and 7.5 < 10 < 15 (h < a < b), two triangles can be formed. ...
Sec. 2.7: Prove Angle Pair Relationships
... Linear pairs of angles are supplementary. Since angles 1 and 2 are a linear pair, then they are supplementary by the Linear Pair Theorem. The same can be said about any other linear pair ...
... Linear pairs of angles are supplementary. Since angles 1 and 2 are a linear pair, then they are supplementary by the Linear Pair Theorem. The same can be said about any other linear pair ...