math144exercises1-2
... the hypotenuse, which is (½, ½). Show that L either goes through the vertex (0, 0) or else contains a point on one of the other two sides. It might be helpful to break this problem up into cases depending upon the slope m of the line, which might be equal to 1, greater than 1, undefined, less than – ...
... the hypotenuse, which is (½, ½). Show that L either goes through the vertex (0, 0) or else contains a point on one of the other two sides. It might be helpful to break this problem up into cases depending upon the slope m of the line, which might be equal to 1, greater than 1, undefined, less than – ...
8.G.5 11.29.12
... Have students write a set of instructions that describe how to create a pair of parallel lines cut by a transversal. Have students read their instructions aloud to a partner and have the partner follow the instructions to ensure that they are accurate. Break students into groups. Provide students wi ...
... Have students write a set of instructions that describe how to create a pair of parallel lines cut by a transversal. Have students read their instructions aloud to a partner and have the partner follow the instructions to ensure that they are accurate. Break students into groups. Provide students wi ...
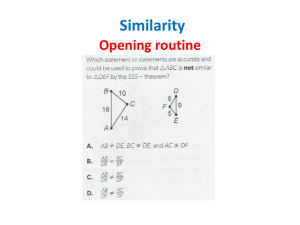
Math 8 Lesson Plan 27 Similar Polygons class outline for students
... was 7.8 meters long into 12 pieces of (-2, -1) in point-slope form, slopeequal length. What was the length of intercept form and standard form. each piece? ...
... was 7.8 meters long into 12 pieces of (-2, -1) in point-slope form, slopeequal length. What was the length of intercept form and standard form. each piece? ...
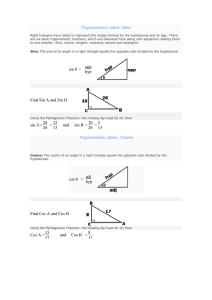
sin θ = opp hyp Find Sin A and Sin B sin A = 24 26 = 12 13 and sin B
... Right triangles have ratios to represent the angles formed by the hypotenuse and its legs. There are six basic trigonometric functions, which are tabulated here along with equations relating them to one another: Sine, cosine, tangent, cosecant, secant and cotangent. Sine: The sine of an angle in a r ...
... Right triangles have ratios to represent the angles formed by the hypotenuse and its legs. There are six basic trigonometric functions, which are tabulated here along with equations relating them to one another: Sine, cosine, tangent, cosecant, secant and cotangent. Sine: The sine of an angle in a r ...
TRIANGLES
... 3. Same side interior angles/co-interior angles are _____________________ 4. Congruent means: ___________________________ ...
... 3. Same side interior angles/co-interior angles are _____________________ 4. Congruent means: ___________________________ ...