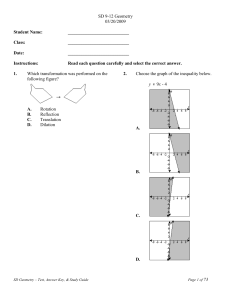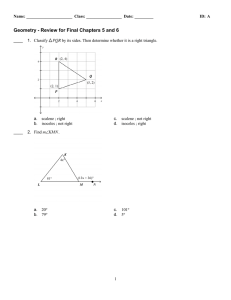
optimal angle bounds for quadrilateral meshes
... common endpoint where they meet with interior angle 90◦ . Any two such are Möbius equivalent. A Carleson quadrilateral is bounded by one finite length hyperbolic segment and two geodesic rays, again with both interior angles equal 90◦ . See Figure 3. It is determined up to isometry by the hyperboli ...
... common endpoint where they meet with interior angle 90◦ . Any two such are Möbius equivalent. A Carleson quadrilateral is bounded by one finite length hyperbolic segment and two geodesic rays, again with both interior angles equal 90◦ . See Figure 3. It is determined up to isometry by the hyperboli ...
Number Algebra Shape, space and measures Handling data G write
... draw line y = 12 to find x values of points of intersection, & write down equation in x with solutions as found above solve simple inequalities: 5<2n≤12, for integer n solve 5x - 2 < 4 solve 5x < 3x + 9 distance-time graph: average speed (km/h) over time in minutes show that a2 + b2 is not always ev ...
... draw line y = 12 to find x values of points of intersection, & write down equation in x with solutions as found above solve simple inequalities: 5<2n≤12, for integer n solve 5x - 2 < 4 solve 5x < 3x + 9 distance-time graph: average speed (km/h) over time in minutes show that a2 + b2 is not always ev ...