Unit 3 Syllabus: Congruent Triangles
... It means that if you put the two triangles on top of each other, they would match up perfectly 5. Triangle congruence works the same as it did for the pentagons, and for all polygons. 6. Given ∆HIJ ≅ ∆MNO . Name all congruent sides and all congruent angles. ...
... It means that if you put the two triangles on top of each other, they would match up perfectly 5. Triangle congruence works the same as it did for the pentagons, and for all polygons. 6. Given ∆HIJ ≅ ∆MNO . Name all congruent sides and all congruent angles. ...
6-6 Congruent Triangles
... If two sides and the included angle of one triangle are congruent to the corresponding parts of another triangle, the triangles are congruent. (The included angle is the angle formed by the ...
... If two sides and the included angle of one triangle are congruent to the corresponding parts of another triangle, the triangles are congruent. (The included angle is the angle formed by the ...
D. bisector of an angle 2. If T is the midpoint of and V lies between R
... When the triangle was reflected, the height of the resulting triangle is parallel to the height of the original triangle. When the triangle was reflected, the base of the resulting triangle lies on the same line as the base of the original triangle. When the triangle was reflected, the corresponding ...
... When the triangle was reflected, the height of the resulting triangle is parallel to the height of the original triangle. When the triangle was reflected, the base of the resulting triangle lies on the same line as the base of the original triangle. When the triangle was reflected, the corresponding ...
parallel lines
... Proof and Perpendicular Lines Review of 2.5 A two-column proof has numbered ____________________ on one side, and _______________ that show the logical order of an argument on the ...
... Proof and Perpendicular Lines Review of 2.5 A two-column proof has numbered ____________________ on one side, and _______________ that show the logical order of an argument on the ...
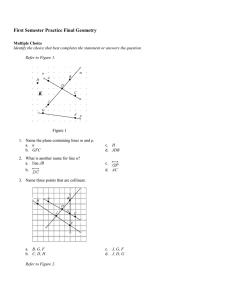
Geometry Semester 1 Final Semester 1 Practice Final
... The first statement column in a truth table contains half Ts, half Fs, grouped together. The second statement column in a truth table contains the same, but they are grouped by half the number that the first column was. The third statement column contains the same but they are grouped by half the nu ...
... The first statement column in a truth table contains half Ts, half Fs, grouped together. The second statement column in a truth table contains the same, but they are grouped by half the number that the first column was. The third statement column contains the same but they are grouped by half the nu ...
The Effect of Dynamic Geometry Software_Redacted A+ 81
... education may have had its ebbs and flows during the second half of the 20th century (Whiteley, 1999) before this time it was considered the dominant force in mathematics education, with Euclid’s Elements forming the basis for the majority of the curriculum. It is perhaps unsurprising that this shou ...
... education may have had its ebbs and flows during the second half of the 20th century (Whiteley, 1999) before this time it was considered the dominant force in mathematics education, with Euclid’s Elements forming the basis for the majority of the curriculum. It is perhaps unsurprising that this shou ...