10.4 Practice with Examples
... Use angles formed by tangents and chords to solve problems in geometry and use angles formed by lines that intersect a circle to solve problems VOCABULARY Theorem 10.12 If a tangent and a chord intersect at a point on a circle, then the measure of each angle formed is one half the measure of its int ...
... Use angles formed by tangents and chords to solve problems in geometry and use angles formed by lines that intersect a circle to solve problems VOCABULARY Theorem 10.12 If a tangent and a chord intersect at a point on a circle, then the measure of each angle formed is one half the measure of its int ...
Non-Euclidean Geometries
... The Most Controversial The Parallel Postulate: In layman’s terms * Given a line and a point not on that line, there is exactly one line through the point that is parallel to the line. ...
... The Most Controversial The Parallel Postulate: In layman’s terms * Given a line and a point not on that line, there is exactly one line through the point that is parallel to the line. ...
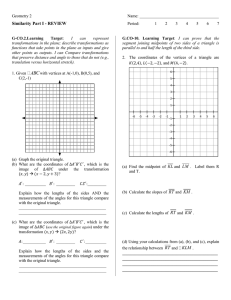
Geometry 2 Name: Similarity Part I - REVIEW Period: 1 2 3 4 5 6 7 G
... represent transformations in the plane; describe transformations as functions that take points in the plane as inputs and give other points as outputs. I can Compare transformations that preserve distance and angle to those that do not (e.g., translation versus horizontal stretch). ...
... represent transformations in the plane; describe transformations as functions that take points in the plane as inputs and give other points as outputs. I can Compare transformations that preserve distance and angle to those that do not (e.g., translation versus horizontal stretch). ...
Equilateral triangle: A triangle with 3 sides the same length
... Line of Symmetry: A line that if a shape is folded over this line the two halves of the shape would match exactly. Rotation Symmetry: A shape has rotation symmetry if it can be rotated less than a full turn around its center point to a position where it looks exactly as it did before it was rotated ...
... Line of Symmetry: A line that if a shape is folded over this line the two halves of the shape would match exactly. Rotation Symmetry: A shape has rotation symmetry if it can be rotated less than a full turn around its center point to a position where it looks exactly as it did before it was rotated ...