Answer
... The vertices of ABC are A(–3, 7), B(–1, 0), and C(5, 5). Graph the triangle and the image of ABC after a translation 4 units right and 5 units down. This translation can be written as the ordered pair (4, –5). To find the coordinates of the translated image, add 4 to each x-coordinate and add –5 ...
... The vertices of ABC are A(–3, 7), B(–1, 0), and C(5, 5). Graph the triangle and the image of ABC after a translation 4 units right and 5 units down. This translation can be written as the ordered pair (4, –5). To find the coordinates of the translated image, add 4 to each x-coordinate and add –5 ...
ppt
... Solve triangle ABC if A 50º, C 33.5º, and b 76. Keep in mind that we must be given one of the three ratios to apply the Law of Sines. In this example, we are given that b 76 and we found that B 96.5º. Thus, we use the ratio b/sin B, or 76/sin96.5º, to find the other two sides. Use the Law ...
... Solve triangle ABC if A 50º, C 33.5º, and b 76. Keep in mind that we must be given one of the three ratios to apply the Law of Sines. In this example, we are given that b 76 and we found that B 96.5º. Thus, we use the ratio b/sin B, or 76/sin96.5º, to find the other two sides. Use the Law ...
Key Concepts, continued
... fundamental relationship between basic terms of geometry. Postulates are accepted as true without proof. •Conjecture: an educated guess based on known information 1.8.1: Proving the Vertical Angles Theorem ...
... fundamental relationship between basic terms of geometry. Postulates are accepted as true without proof. •Conjecture: an educated guess based on known information 1.8.1: Proving the Vertical Angles Theorem ...
Unit 5 Similarity and Triangles
... 1. How can you determine whether two figures are similar using similarity transformations, angle measures, and side lengths? 2. What is the AA Similarity theorem and why does it sufficiently determine whether two triangles are similar or not? 3. How can you prove that a line parallel to one side of ...
... 1. How can you determine whether two figures are similar using similarity transformations, angle measures, and side lengths? 2. What is the AA Similarity theorem and why does it sufficiently determine whether two triangles are similar or not? 3. How can you prove that a line parallel to one side of ...
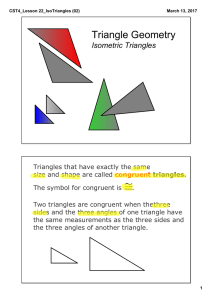
CST4_Lesson 22_IsoTriangles (02)
... corresponding congruent angle contained between two congruent corresponding sides are isometric. 2. Theorem of Congruence ASA: Two triangles with corresponding congruent side contained between two congruent corresponding angles are isometric. 3. Theorem of Congruence SSS: Two triangles with corr ...
... corresponding congruent angle contained between two congruent corresponding sides are isometric. 2. Theorem of Congruence ASA: Two triangles with corresponding congruent side contained between two congruent corresponding angles are isometric. 3. Theorem of Congruence SSS: Two triangles with corr ...