Properties and defintions File - Wynberg Moodle
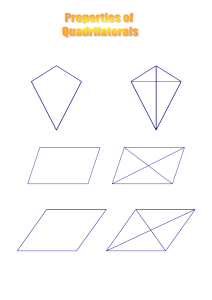
... Considering the definitions you have been given, and using your ruler, protractor etc, draw one example of each kind of quadrilateral on the coloured paper, as listed. In each case your diagram should be about 9 cm across. You must also draw in the diagonals of each quadrilateral. By the end of the ...
... Considering the definitions you have been given, and using your ruler, protractor etc, draw one example of each kind of quadrilateral on the coloured paper, as listed. In each case your diagram should be about 9 cm across. You must also draw in the diagonals of each quadrilateral. By the end of the ...
Holt McDougal Geometry 7-1
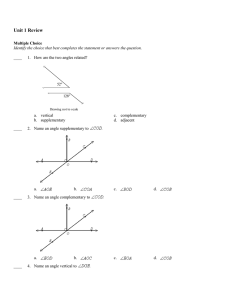
... 1. If ∆QRS ∆ZYX, identify the pairs of congruent angles and the pairs of congruent ...
... 1. If ∆QRS ∆ZYX, identify the pairs of congruent angles and the pairs of congruent ...