Homothetic centers of three circles and their three
... where three angles of elevation are equal to each other. In section 2, we review an easy construction of homothetic centers of two circles. Using the homothetic centers, we will construct the points from where the angles of elevation are equal to each other for two cones in section 3. A relation bet ...
... where three angles of elevation are equal to each other. In section 2, we review an easy construction of homothetic centers of two circles. Using the homothetic centers, we will construct the points from where the angles of elevation are equal to each other for two cones in section 3. A relation bet ...
Geometry Fall 2016 Lesson 017 _Using postulates and theorems to
... Below are the theorems we proved yesterday Theorem - If two angles are right angles, then they are congruent Theorem - If two angles are straight angles, then they are congruent Theorem - If two angles are complements of the same angle, then they are congruent Theorem - If two angles are sup ...
... Below are the theorems we proved yesterday Theorem - If two angles are right angles, then they are congruent Theorem - If two angles are straight angles, then they are congruent Theorem - If two angles are complements of the same angle, then they are congruent Theorem - If two angles are sup ...
Trouncing Trig Technicalities
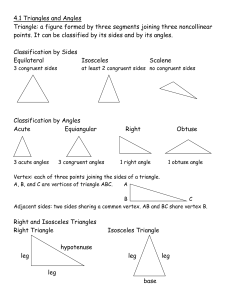
... Triangles can have special names based on their angles and sides. They can also have more than one name — a triangle can be both acute and isosceles, for example. Here are their descriptions, and check out Figure 1-5 for the pictures: ✓ Acute triangle: A triangle where all three angles are acute. ✓ ...
... Triangles can have special names based on their angles and sides. They can also have more than one name — a triangle can be both acute and isosceles, for example. Here are their descriptions, and check out Figure 1-5 for the pictures: ✓ Acute triangle: A triangle where all three angles are acute. ✓ ...
ON EUCLID S FIVE POSTULATES - Revista Brasileira de História
... triangle for every triple of straight lines. Thus, the explicit Euclidean definition alone cannot be transformed into a postulate. We need to reveal a not explicitly mentioned characterization of the triangle. If one looks at the overall structure of the Euclidean definitions, one can recognize an u ...
... triangle for every triple of straight lines. Thus, the explicit Euclidean definition alone cannot be transformed into a postulate. We need to reveal a not explicitly mentioned characterization of the triangle. If one looks at the overall structure of the Euclidean definitions, one can recognize an u ...
Geometry 2009 SOL
... • Our eyes tell us that 1 and 2 are small acute angles • Plug in answers: only F and G give small acute angles Vertical angles are equal 6x + 12 = 9x – 4 6x + 16 = 9x 16 = 3x 16/3 = x ...
... • Our eyes tell us that 1 and 2 are small acute angles • Plug in answers: only F and G give small acute angles Vertical angles are equal 6x + 12 = 9x – 4 6x + 16 = 9x 16 = 3x 16/3 = x ...