Document
... 13. Another proposed wheelchair ramp is shown. What is the rise of this ramp? If necessary, round your answer to the nearest inch. ...
... 13. Another proposed wheelchair ramp is shown. What is the rise of this ramp? If necessary, round your answer to the nearest inch. ...
Similarity, Congruence and Proofs - 3
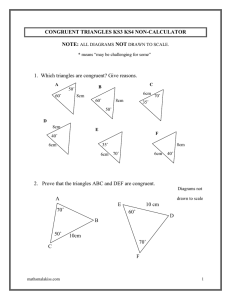
... Since we have learned some basics about congruence in our previous lesson, we can use that to begin writing proofs. Watch this video to see an example of proving two triangles congruent . We can also prove congruence with other polygons and shapes, for example, line segments. When we begin doing pro ...
... Since we have learned some basics about congruence in our previous lesson, we can use that to begin writing proofs. Watch this video to see an example of proving two triangles congruent . We can also prove congruence with other polygons and shapes, for example, line segments. When we begin doing pro ...