PPT
... entropic time asymmetry) there is no information (that's why Maxwell's demon can't function) so there could be no minds whatever. • The low-entropy property of the past is needed to allow some information about it to be conveyed with a relatively small number of bits. I.e. a photograph of some place ...
... entropic time asymmetry) there is no information (that's why Maxwell's demon can't function) so there could be no minds whatever. • The low-entropy property of the past is needed to allow some information about it to be conveyed with a relatively small number of bits. I.e. a photograph of some place ...
Day 58 - Tahoma
... More microstates Increased entropy! If we increase temperature, the average kinetic energy increases. Greater distribution of molecular speeds More possible kinetic energy values More microstates Increasing entropy ...
... More microstates Increased entropy! If we increase temperature, the average kinetic energy increases. Greater distribution of molecular speeds More possible kinetic energy values More microstates Increasing entropy ...
Quantum Field Theory
... How do operators and quantum fields transform? Lorentz transformation (proper, orthochronous) is represented by a unitary operator that must obey the composition rule: ...
... How do operators and quantum fields transform? Lorentz transformation (proper, orthochronous) is represented by a unitary operator that must obey the composition rule: ...
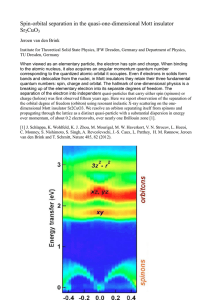
Spin-orbital separation in the quasi-one
... When viewed as an elementary particle, the electron has spin and charge. When binding to the atomic nucleus, it also acquires an angular momentum quantum number corresponding to the quantized atomic orbital it occupies. Even if electrons in solids form bands and delocalize from the nuclei, in Mott i ...
... When viewed as an elementary particle, the electron has spin and charge. When binding to the atomic nucleus, it also acquires an angular momentum quantum number corresponding to the quantized atomic orbital it occupies. Even if electrons in solids form bands and delocalize from the nuclei, in Mott i ...
PHY 104: Modern Physics - Physlab
... pigments have the colors that they do, why are some materials hard and others soft, why do metals, for example, conduct electricity and heat easily, while glass doesn’t. Quantum physics also forms the basis of our understanding of the chemical world, materials science, as well as electronic devices ...
... pigments have the colors that they do, why are some materials hard and others soft, why do metals, for example, conduct electricity and heat easily, while glass doesn’t. Quantum physics also forms the basis of our understanding of the chemical world, materials science, as well as electronic devices ...
Physics 120 Homework Set #1 (due Sunday
... b) Explain how Einstein’s equations for the energy and momentum of light quanta were used by De Broglie to encapsulate this duality. c) Identify the particle and wave aspects of each of these equations. a) Particle-wave duality corresponds to the observation that different experiments or observation ...
... b) Explain how Einstein’s equations for the energy and momentum of light quanta were used by De Broglie to encapsulate this duality. c) Identify the particle and wave aspects of each of these equations. a) Particle-wave duality corresponds to the observation that different experiments or observation ...
Activity 2 - The Bohr Atom
... Experiments by Geiger and Marsden, the ‘Gold-foil’ or ‘Rutherford’ experiment showed that almost all the mass and positive charge of the nucleus was concentrated into a tiny sphere at the centre of the atom, which prompted Rutherford’s planetary model, of electrons orbiting the nucleus, like planets ...
... Experiments by Geiger and Marsden, the ‘Gold-foil’ or ‘Rutherford’ experiment showed that almost all the mass and positive charge of the nucleus was concentrated into a tiny sphere at the centre of the atom, which prompted Rutherford’s planetary model, of electrons orbiting the nucleus, like planets ...
12/6/16 - Physics
... . (m v) > h Δ x Δ h = 6.6 x 10-34 Joule-s Note: Some people think of the width fo the wavefunction as being the size of the particle. If so, particles do not have an inherent “size”. They are wave-like and spread out according to their “container” (forces) -- an electron can be microscopic ...
... . (m v) > h Δ x Δ h = 6.6 x 10-34 Joule-s Note: Some people think of the width fo the wavefunction as being the size of the particle. If so, particles do not have an inherent “size”. They are wave-like and spread out according to their “container” (forces) -- an electron can be microscopic ...
Quantum Complexity and Fundamental Physics
... RESOLVED: That the results of quantum complexity research can deepen our understanding of physics. That this represents an intellectual payoff from quantum computing, whether or not scalable QCs are ever built. ...
... RESOLVED: That the results of quantum complexity research can deepen our understanding of physics. That this represents an intellectual payoff from quantum computing, whether or not scalable QCs are ever built. ...
Presentation (PowerPoint File)
... decoherence through error correction and fault-tolerant computation. 5. Measurement: The ability to read out the state of the computer in a convenient product basis. ...
... decoherence through error correction and fault-tolerant computation. 5. Measurement: The ability to read out the state of the computer in a convenient product basis. ...
presentation source
... the systems we are interested in has many available quantum states - many states can have identical energy --> multiplicity (degeneracy) of a level: number of quantum states with the same energy - it is the number of quantum states that is important in thermal physics, not the number of energy level ...
... the systems we are interested in has many available quantum states - many states can have identical energy --> multiplicity (degeneracy) of a level: number of quantum states with the same energy - it is the number of quantum states that is important in thermal physics, not the number of energy level ...
Lecture 4
... “cubic” lattice in 3N dimensional momentum space with cube edge h/L and so the volume of phase space per state is (h/L)3N L3N = h3N . The factor of N ! arises because from quantum mechanics we recognize that identical particles are indistinguishable. In a two-particle, one-dimensional system, for ex ...
... “cubic” lattice in 3N dimensional momentum space with cube edge h/L and so the volume of phase space per state is (h/L)3N L3N = h3N . The factor of N ! arises because from quantum mechanics we recognize that identical particles are indistinguishable. In a two-particle, one-dimensional system, for ex ...