ExamView - SCA 1 Review.tst
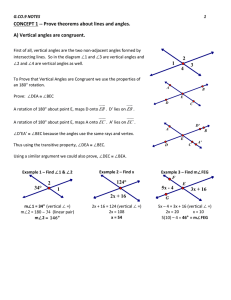
... The angles are corresponding angles and they are congruent, so the lanes are parallel by the Converse of the Corresponding Angles Postulate. 3x + 4 = 3(10) + 4 = 34°; 4x − 6 = 4(10) − 6 = 34° The angles are same-side interior angles and they are supplementary, so the lanes are parallel by the Conver ...
... The angles are corresponding angles and they are congruent, so the lanes are parallel by the Converse of the Corresponding Angles Postulate. 3x + 4 = 3(10) + 4 = 34°; 4x − 6 = 4(10) − 6 = 34° The angles are same-side interior angles and they are supplementary, so the lanes are parallel by the Conver ...
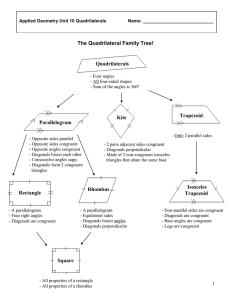
properties of quadrilaterals
... 1. All the properties of a parallelogram apply by definition. 2. All angles are right angles. 3. The diagonals are congruent. Properties of Kites In a kite, 1. Two disjoint pairs of consecutive sides are congruent by definition. 2. The diagonals are perpendicular. 3. One diagonal is the perpendicula ...
... 1. All the properties of a parallelogram apply by definition. 2. All angles are right angles. 3. The diagonals are congruent. Properties of Kites In a kite, 1. Two disjoint pairs of consecutive sides are congruent by definition. 2. The diagonals are perpendicular. 3. One diagonal is the perpendicula ...
Non-Euclidean Geometry and a Little on How We Got Here
... Consider a circle of radius 1, in which we inscribe a regular polygon of 3×2n−1 sides, with semiperimeter bn , and superscribe a regular polygon of 3 × 2n−1 sides, with semiperimeter an . The diagram for the case n = 2 is on the right. T The effect of this procedure is to define an increasing sequen ...
... Consider a circle of radius 1, in which we inscribe a regular polygon of 3×2n−1 sides, with semiperimeter bn , and superscribe a regular polygon of 3 × 2n−1 sides, with semiperimeter an . The diagram for the case n = 2 is on the right. T The effect of this procedure is to define an increasing sequen ...