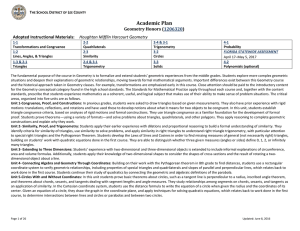
File
... each radius so the two tangents intersect at point N. Measure the distance from N to each point of tangency. What do you notice? b) Compare your answer to part a with that of your classmates. How do the lengths of two tangents drawn to a circle from the same point outside the circle appear to be rel ...
... each radius so the two tangents intersect at point N. Measure the distance from N to each point of tangency. What do you notice? b) Compare your answer to part a with that of your classmates. How do the lengths of two tangents drawn to a circle from the same point outside the circle appear to be rel ...
notes
... Angle-Angle-Side (AAS) AAS stands for “Angle-Angle-Side” and states that two triangles are congruent if two triangles with two known angle measures and the non-included side length are congruent. ...
... Angle-Angle-Side (AAS) AAS stands for “Angle-Angle-Side” and states that two triangles are congruent if two triangles with two known angle measures and the non-included side length are congruent. ...
Chapter 8: Quadrilaterals
... 1. How do the measures of opposite sides compare? 2. Measure the distance between the top and bottom straws in at least three places. Then measure the distance between the left and right straws in at least three places. What seems to be true about the opposite sides? 3. Shift the position of the sid ...
... 1. How do the measures of opposite sides compare? 2. Measure the distance between the top and bottom straws in at least three places. Then measure the distance between the left and right straws in at least three places. What seems to be true about the opposite sides? 3. Shift the position of the sid ...
C.1 Exploring Congruence and Similarity
... relationships between two lines. Parallel lines are coplanar lines that do not intersect. (Recall that two nonvertical lines are parallel if and only if they have the same slope.) Intersecting lines are coplanar and have exactly one point in common. If intersecting lines meet at right angles, they a ...
... relationships between two lines. Parallel lines are coplanar lines that do not intersect. (Recall that two nonvertical lines are parallel if and only if they have the same slope.) Intersecting lines are coplanar and have exactly one point in common. If intersecting lines meet at right angles, they a ...
History of geometry

Geometry (from the Ancient Greek: γεωμετρία; geo- ""earth"", -metron ""measurement"") arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).Classic geometry was focused in compass and straightedge constructions. Geometry was revolutionized by Euclid, who introduced mathematical rigor and the axiomatic method still in use today. His book, The Elements is widely considered the most influential textbook of all time, and was known to all educated people in the West until the middle of the 20th century.In modern times, geometric concepts have been generalized to a high level of abstraction and complexity, and have been subjected to the methods of calculus and abstract algebra, so that many modern branches of the field are barely recognizable as the descendants of early geometry. (See Areas of mathematics and Algebraic geometry.)